MATH 373 -- Applied Mathematics (PDE)

April 26, 2001

A Boundary Value Problem for the 2D Wave Equation

Circular Membrane: 0 <= r <= a, 0 <= <=

We will solve the following problem

The solution will be a "linear combination" of the fundamental

modes we saw last time. Because the initial displacement is

0 for all only the "cos - sin" and "sin - sin" forms are

necessary. Moreover, because of the form of the initial

velocity, we see that only terms with are

necessary. This means that the expansion will contain only

terms with m = 3. (For more general initial positions and

velocities, terms with more, even infinitely many, different

m values would be necessary.)

We have

,

where is the n th positive zero of the Bessel function .

To find the coefficients , we will use the orthogonality properties

of the functions . Because these are eigenfunctions

of the self-adjoint Sturm-Liouville operator

(the 9 equals ), we know that

if , then .

whenever m <> n. It then follows as usual that in order to find

the expansion of a given in terms of these eigenfunctions,

we will have:

, when

The resulting expansion is called the Fourier-Bessel series for f .

In our problem, taking =

we see that as above, so

To generate a plot, we take a = 1, c = 1,

> a := 1; c := 1;

> alpha := r -> r*(1-r);

> c := n -> evalf(Int(alpha(r)*BesselJ(3,BesselJZeros(3,n)*r/a)*r,r = 0 .. a)/Int(BesselJ(3,BesselJZeros(3,n)*r/a)^2*r,r = 0 .. a)):

> B := n -> a*c[n]/(c*BesselJZeros(3,n)):

As always, to plot, we need to consider a finite partial sum of the Fourier-Bessel

series. How good is our approximation to ?

> plot({alpha(r),add(c(n)*BesselJ(3,BesselJZeros(3,n)*r/a),n=1..10)},r=0..1);

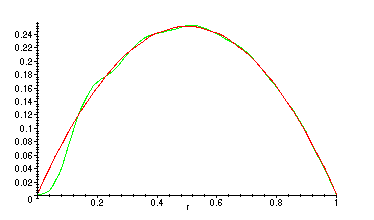
A corresponding partial sum for the series solution of the wave equation:

> PS := k -> add(B(n)*BesselJ(3,BesselJZeros(3,n)*r/a)*sin(3*theta)*sin(c*BesselJZeros(3,n)*t/a),n=1..k);

Warning, `n` in call to `add` is not local

> PS5:=PS(5):

> with(plots):

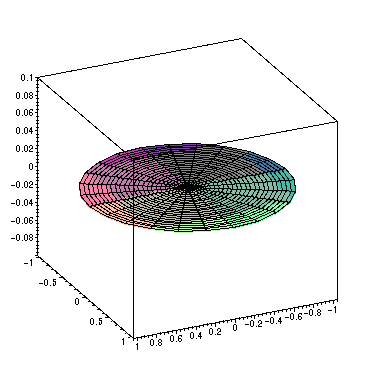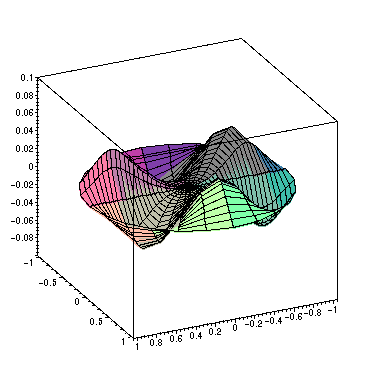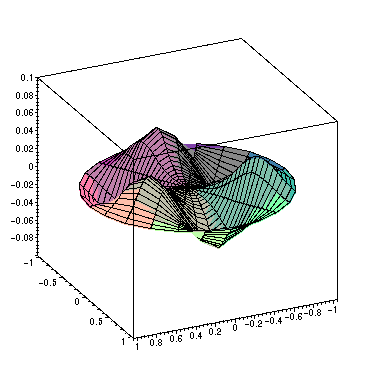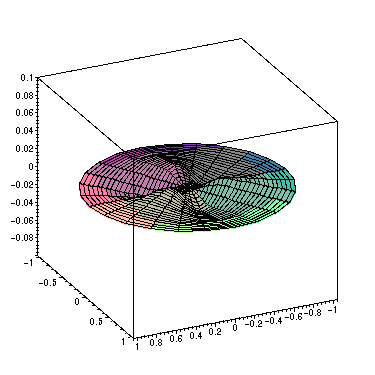
> animate3d([r*cos(theta),r*sin(theta),PS5],r=0..a,theta=0..2*Pi,t=0..2,frames=30,view=-0.1..0.1,axes=BOXED);