Four Vortex Animations

One-parameter Families of Relative Equilibria in the Planar Four-Vortex Problem
Below are some examples of relative equilibria in the planar four-vortex problem with vortex circulations Γ₁ = Γ₂ = 1 (shown in blue), and Γ₃ = Γ₄ = m (shown in red), where m is a parameter and -1 < m ≤ 1. The distances have been scaled so that the distance between the first and second vortices is always one. Each configuration is an initial condition for a circular periodic orbit in the planar four-vortex problem. (The actual motion of each member in the family is a rigid rotation about the center of vorticity.) Animations written using Maple 15.

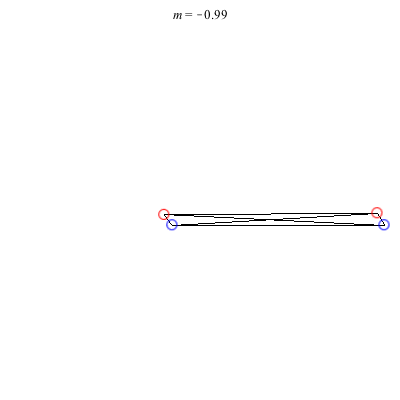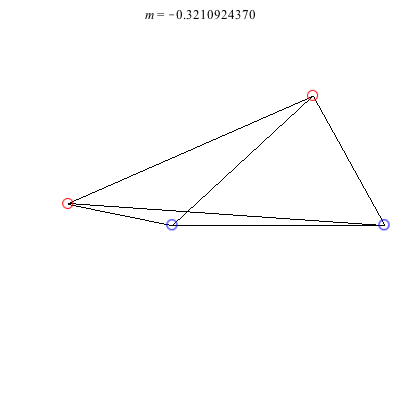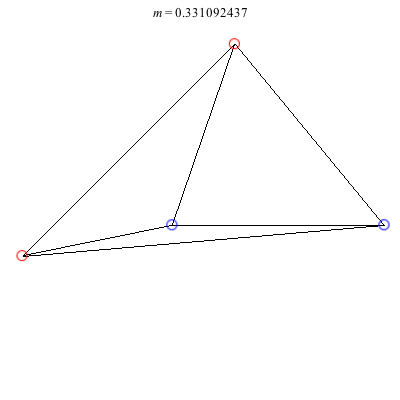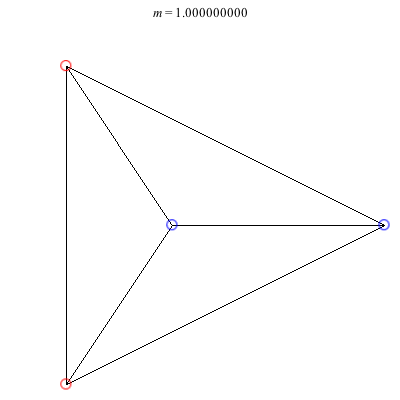
1) Asymmetric: This family of asymmetric relative equilibria is convex for m < 0 and concave for m > 0, with three of the vortices becoming collinear at m = 0. The configuration for m = 1 is symmetric and also degenerate. It consists of three vortices located at the vertices of an equilateral triangle and a fourth vortex at the center. Other than some asymmetric collinear configurations, these are the only asymmetric solutions for these (symmetric) choices of circulations.

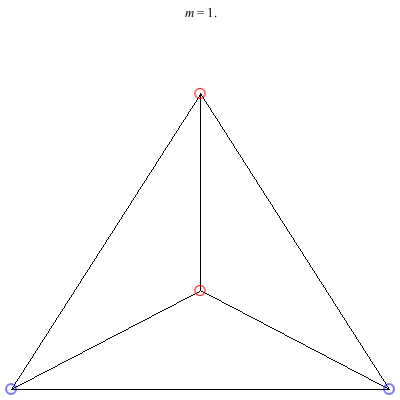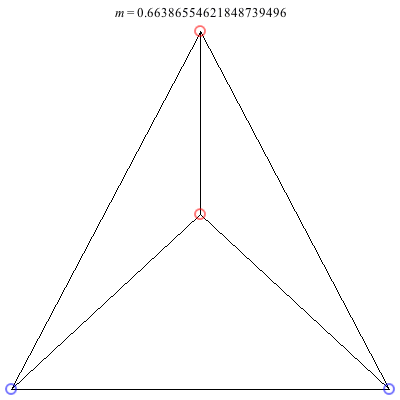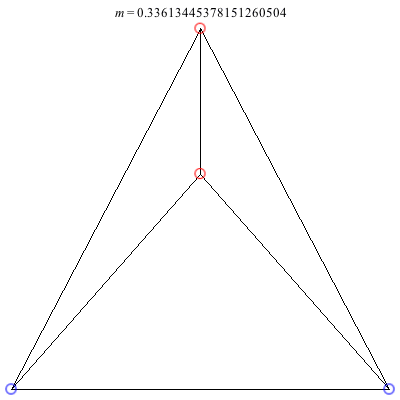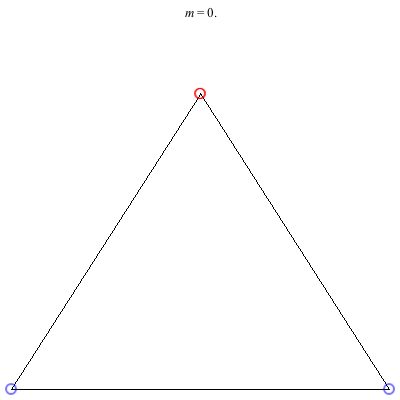
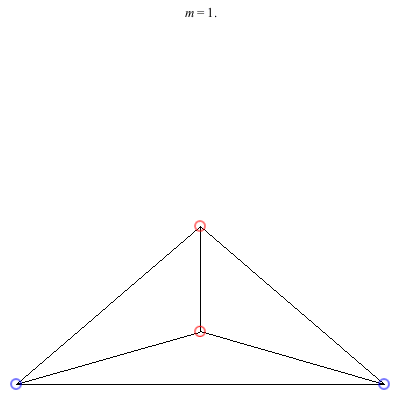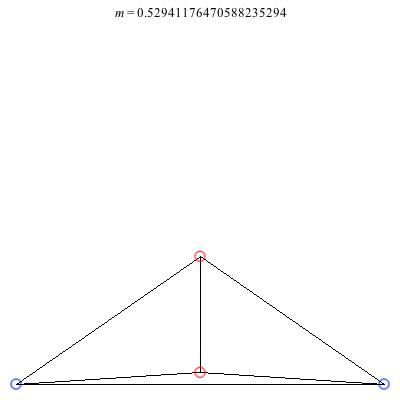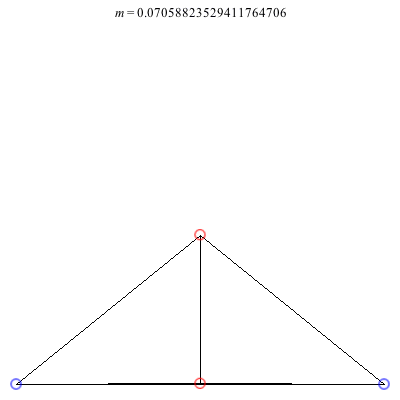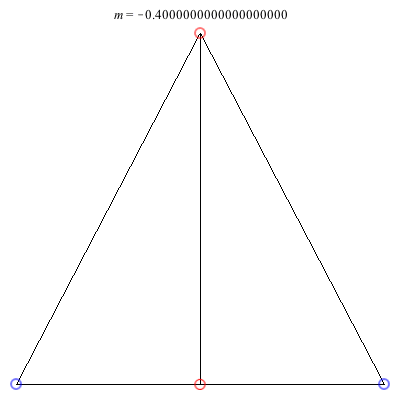
2) Kites: Above are two families of kite configurations where vortices 3 and 4 are on the axis of symmetry. Both families begin at m = 1 with the equilateral triangle plus a vortex at the center solution. The family on the left exists only for 0 < m ≤ 1. As m decreases toward 0, the distance between the third and fourth vortex goes to 0, while the shape of the exterior triangle becomes equilateral. The family on the right exists for -1/2 < m ≤ 1. It is concave for m > 0 and convex for m < 0, with three vortices becoming collinear at m = 0. The convex configurations all have three vortices very close to being collinear, and as m decreases toward -1/2, the distance between the third and fourth vortex goes to infinity.

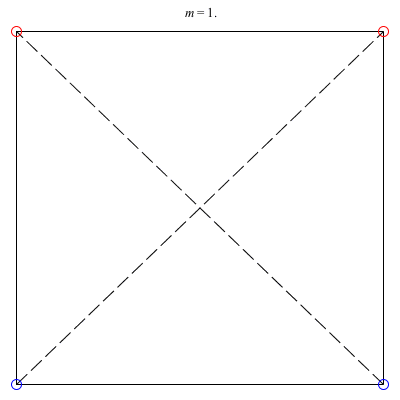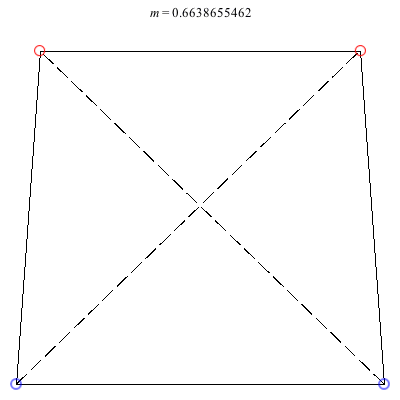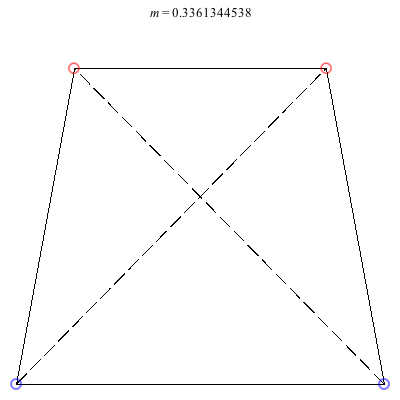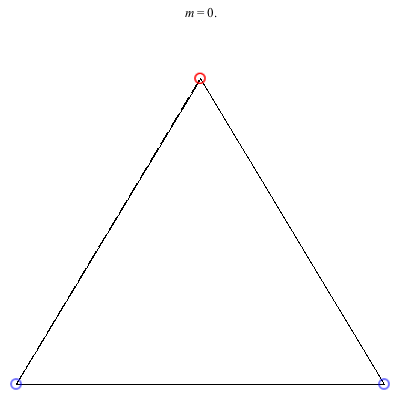
3) Isosceles Trapezoid: The isosceles trapezoid family above exists for 0 < m ≤ 1. Beginning with a square at m = 1, the length of the shorter base monotonically decreases to 0 as m decreases, ending in an equilateral triangle with vortices 3 and 4 colliding at m = 0. The ratio of the common side-length to the larger base starts at 1 at the square configuration and decreases to approximately 0.904781 when m ≈ 0.234658, before increasing back to 1 when m = 0. This family is always stable.

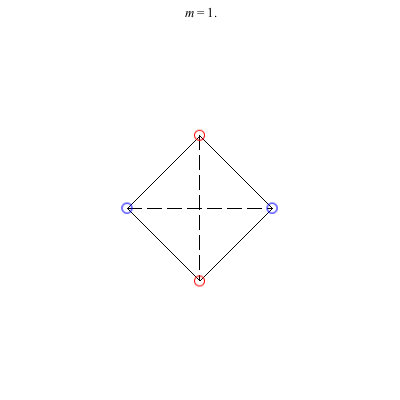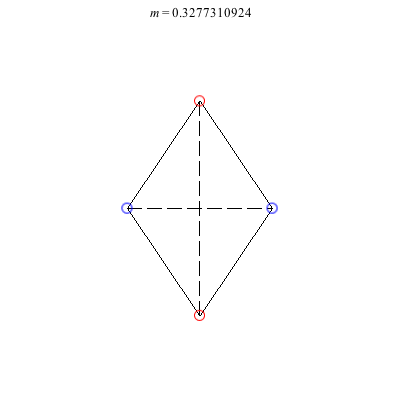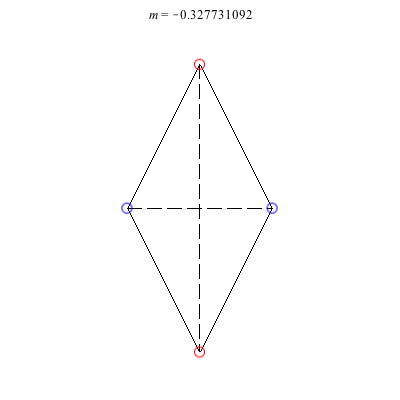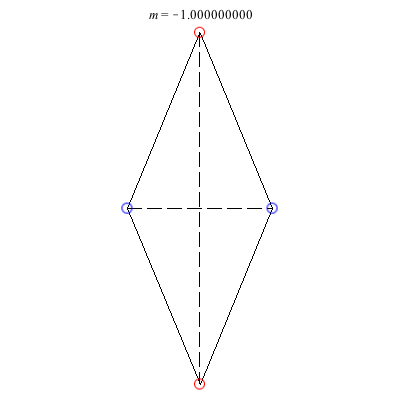
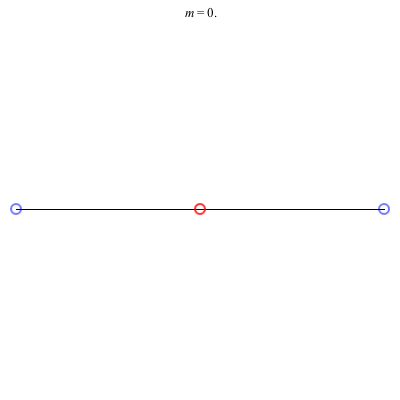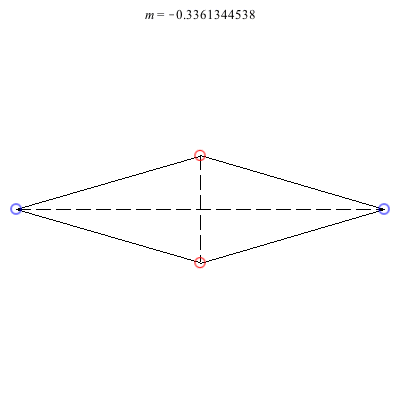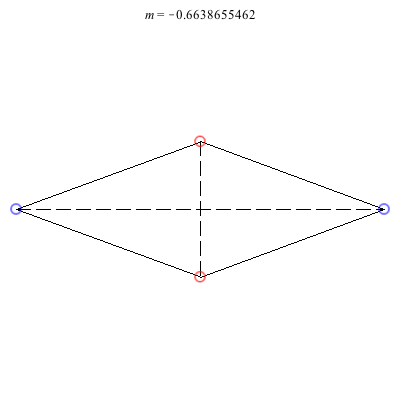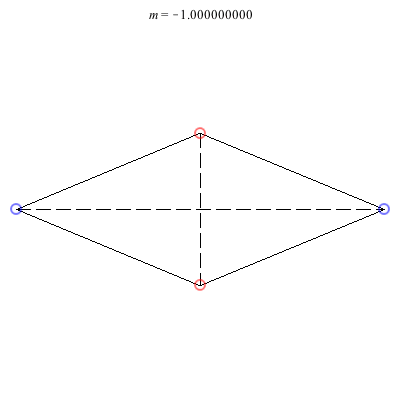
4) Rhombii: Above are two families of rhombii relative equilibria. The family on the left exists for -1 ≤ m ≤ 1, with the larger strength vortices lying on the shorter diagonal. Starting with a square at m = 1, the ratio of the longer diagonal to the shorter increases in length as m decreases, ending with a maximum length of $\sqrt{2}$ + 1 at m = -1. This family is linearly stable for -2 + $\sqrt{3}$ < m ≤ 1. When m = -2 + $\sqrt{3}$ , the total angular vortex momentum is zero and the relative equilibrium is degenerate. For -1 < m < -2 + $\sqrt{3}$ , it is unstable.

The rhombus family on the right exists for -1 ≤ m < 0 , with the larger (positive) strength vortices situated on the longer diagonal. This family emerges from a collinear collision (Euler) configuration where vortices 3 and 4 have merged together at a point equidistant from vortices 1 and 2. As m decreases, the ratio of the shorter diagonal to the longer grows in size monotonically until reaching a maximum of $\sqrt{2}$ - 1 at m = -1. Interestingly, the rhombus becomes an actual equilibrium at m = -2 + $\sqrt{3}$ , and for m < -2 + $\sqrt{3}$ , the direction of rotation flips. This family is always unstable. However, it undergoes a pitchfork bifurcation at m = m*, where m* is the only real root of the cubic 9m³ + 3m² + 7m + 5. As m decreases through this value, one pair of real eigenvalues meets at the origin and then becomes a pure imaginary pair. Two convex kite relative equilibria are born in the pitchfork bifurcation with vortices 1 and 2 on the axis of symmetry.