Exercises

In these exercises we will be working with exponential and logarithm functions expressed in terms of the irrational number e. It is the base that is used most frequently in science and mathematics. The first 20 digits in its decimal expansion are 2.7182818284590452354. The function 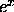is sometimes written 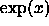, in a manner similar to .

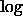1. Let us begin by working with the particular function .
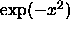   1. Without using a calculator, plot the graph of 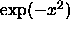. In particular, think about particular values near the origin and think about its behavior as 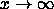and .
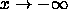   2. Describe the behavior of the plot in words. What are its features?
2. Now let 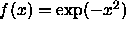. We want to alter f by applying simple algebraic operations to the dependent variable y and the independent variable x. In this exercise we work with the dependent variable.
   1. Define a new function by 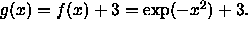Describe how the graph of g compares to the graph of f and graph f and g on the same set of coordinate axes.
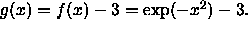   2. Suppose instead we had defined g by Describe how the graph of g compares to the graph of f and graph f and g on the same set of coordinate axes.
   3. In general, if f is a function whose graph you know, how do you obtain the graph of a function g defined by g(x) =f(x) + c from the graph of f? (Treat the cases of c;SPMgt;0 and c;SPMlt;0 separately.)
3. Now, working with the same function, let's multiply the dependent variable by a scalar.
   1. Define a new function by 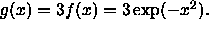Describe how the graph of g compares to the graph of f and graph f and g on the same set of coordinate axes.
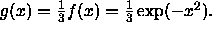   2. Suppose instead we had defined g by Describe how the graph of g compares to the graph of f and graph f and g on the same set of coordinate axes.
   3. In general, if f is a function whose graph you know, how do you obtain the graph of a function g defined by g(x) =cf(x) from the graph of f? (How many different cases should you consider? Treat each one separately.)
4. Now let us switch to working with the independent variable.
   1. Define a new function by 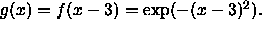Describe how the graph of g compares to the graph of f and graph f and g on the same set of coordinate axes.
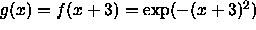   2. Suppose instead we had defined g by . Describe how the graph of g compares to the graph of f and graph f and g on the same set of coordinate axes.
   3. In general, if f is a function whose graph you know, how do you obtain the graph of a function g defined by g(x) =f(x+c) from the graph of f? (Treat the cases of c;SPMgt;0 and c;SPMlt;0 separately.)
5. Now, working with the same function, let's multiply the independent variable by a scalar.
   1. Define a new function by 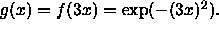Describe how the graph of g compares to the graph of f and graph f and g on the same set of coordinate axes.
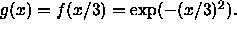   2. Suppose instead we had defined g by Describe how the graph of g compares to the graph of f and graph f and g on the same set of coordinate axes.
   3. In general, if f is a function whose graph you know, how do you obtain the graph of a function g defined by g(x) =f(cx) from the graph of f? (How many different cases should you consider? Treat each one separately.)