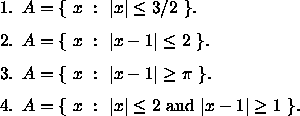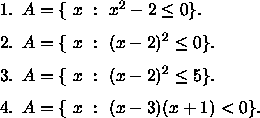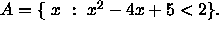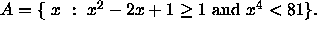Next: Discussion
Up: Discussion
Previous: Discussion
Work through the following together. Be sure that each person in the
group knows how to do the problem and can explain it to the others.
Take turns explaining the problems. Don't be afraid to ask each other
to repeat an explanation. Even if you can do the intermediate steps in your
head, explain them carefully so that you could explain them at the
blackboard. In your write up, write out the intermediate
steps. Everyone in the group should be working on the problems and
writing out solutions. However, one person should be a designated
``scribe'' for the version that you hand in.
- First, let's think about some basic properties of absolute
value.
- If |x| = 3, what does that tell us about x? If |x| = c,
where c represents a real number, what does that tell us about x?
- If
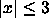 , what does that tell us about x?
, what does that tell us about x?
- The description of each of the following sets A involves inequalities. Rewrite the
set as a union of intervals. (That is, write them in the form
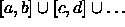 .)
.)
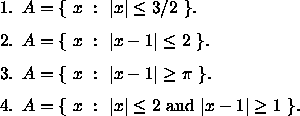
- The description of each of the following sets A involves inequalities. Rewrite the
set as a union of intervals.
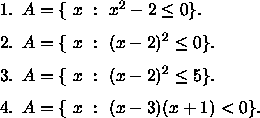
- How do you find the values of x that satisfy a quadratic
equation,
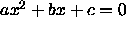 ? What are the possibilities for
solutions to the equation? What do the possibilities depend upon?
What does this have to do with factoring the polynomial?
? What are the possibilities for
solutions to the equation? What do the possibilities depend upon?
What does this have to do with factoring the polynomial?
- Write A as a union of intervals, where
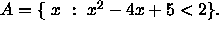
- Write A as a union of intervals, where
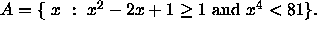
- As a group, think of three examples of descriptions of sets like
the ones we have been doing, but not identical to any of them. (So it
is not enough just to change the numbers.) Write the sets as
intervals, then exchange your examples with those of a neighboring
group. Do those of the other group. We will put some of the
solutions on the board at the end of class.



Next: Discussion
Up: Discussion
Previous: Discussion
Thu Jul 29 16:28:25 EDT 1999
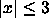 , what does that tell us about x?
, what does that tell us about x?