


Next: Discussion
Up: Discussion
Previous: Discussion
- For each of the following functions h, (i) identify
functions f and g so that h=f(g(x)). (ii) Find h'(x).
-
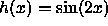 .
. -
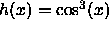 .
. -
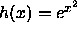 .
.
- Each of the following functions h is a nested composition of more
than two functions. (i) identify all the functions that are used to
make h. (ii) Find h'(x) by applying the chain rule two or more times.
-
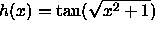 .
. -
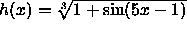 .
. -
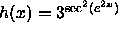
- We can also use the chain rule to find the derivative of
the function g if we know the function f. Let's consider two
examples.
- We know that
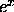 and
and 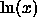 are inverse functions, so that
are inverse functions, so that
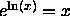 . By differentiating both sides of this equation
(applying the chain rule to the left side), find a formula for the
derivative of the natural logarithm function.
. By differentiating both sides of this equation
(applying the chain rule to the left side), find a formula for the
derivative of the natural logarithm function. - We know that
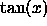 and
and 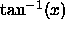 are inverse functions,
so that
are inverse functions,
so that 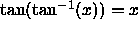 . By differentiating both sides of this
equation (applying the chain rule to the left side), find a formula
for the derivative of the inverse tangent function. (Hint:
Your final answer should contain no trig functions. To
obtain the final form of the derivative of
. By differentiating both sides of this
equation (applying the chain rule to the left side), find a formula
for the derivative of the inverse tangent function. (Hint:
Your final answer should contain no trig functions. To
obtain the final form of the derivative of 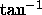 , you will have
to use facts from trigonometry.)
, you will have
to use facts from trigonometry.) - Now let us consider the general case. Suppose that f and g
are inverse functions, so that f(g(x)) =x. By differentiating both sides of this
equation (applying the chain rule to the left side), find a formula
for the derivative of g, the inverse function of f.
Thu Jul 29 16:28:25 EDT 1999
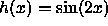 .
.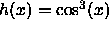 .
.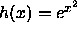 .
.
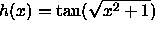 .
.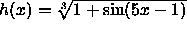 .
.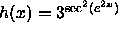
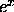 and
and 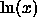 are inverse functions, so that
are inverse functions, so that
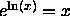 . By differentiating both sides of this equation
(applying the chain rule to the left side), find a formula for the
derivative of the natural logarithm function.
. By differentiating both sides of this equation
(applying the chain rule to the left side), find a formula for the
derivative of the natural logarithm function.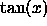 and
and 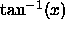 are inverse functions,
so that
are inverse functions,
so that 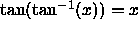 . By differentiating both sides of this
equation (applying the chain rule to the left side), find a formula
for the derivative of the inverse tangent function. (Hint:
Your final answer should contain no trig functions. To
obtain the final form of the derivative of
. By differentiating both sides of this
equation (applying the chain rule to the left side), find a formula
for the derivative of the inverse tangent function. (Hint:
Your final answer should contain no trig functions. To
obtain the final form of the derivative of 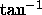 , you will have
to use facts from trigonometry.)
, you will have
to use facts from trigonometry.)