Exercises

1. 1. Suppose that a polynomial of degree 2 can be factored into 3(x-1)(x+2). Describe how to sketch the graph of f(x) = 3(x- 1)(x+2) from the information of this formula. In particular, how do we know when f is positive, negative, and zero? How do we know what happens to the values of f as 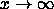and ?
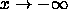   2. Suppose that instead we have -3(x-1)(x+2). How would this change your answer to (a)?
2. 1. Suppose that 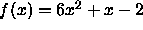. Factor f and write it in the form A(x- B)(x - C). Use this form to sketch the graph of f.
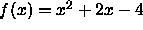   2. Suppose . Can f be factored? If not, explain why not, if so, find the factors, and sketch the graph of f.
3. Formulate a general procedure for plotting the graph of polynomials of degree 2 that can be factored in the form A(x- B)(x - C). Does this procedure work for all polynomials of degree 2? Why or why not?
4. Now let us consider polynomials of degree 3. Suppose f(x) = (x-1)(x+1)(x+2).
   1. When is f positive? negative? zero?
   2. What happens to the values of f as 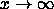and ?
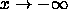   3. Use this information to sketch the graph of f.
5. Repeat Exercise 4 for the function .
6. 1. Formulate a general rule for describing the graph of a cubic polynomial that factors as

      

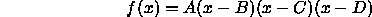
      where 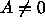and B, C, and D are not equal to each other.

   2. How does your answer change if two of B, C, and D are equal? if B=C=D?
   3. Does this procedure work for all polynomials of degree 3? Why or why not?