- What are the domains and ranges of the function
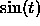 and
and
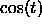 ? Do the amplitudes of
? Do the amplitudes of 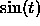 and
and 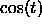 have
anything to do with their domains or ranges? If so, explain.
have
anything to do with their domains or ranges? If so, explain. - Which points on the circle in Figure 1.65 correspond to where
the graph of the
 function crosses the x-axis? Which points
on the circle correspond to where the graph the
function crosses the x-axis? Which points
on the circle correspond to where the graph the  function has
maximum values and minimum values?
function has
maximum values and minimum values? - Which points on the circle in Figure 1.65 correspond to where
the graph of the
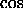 function crosses the x-axis? Which points
on the circle correspond to where the graph the
function crosses the x-axis? Which points
on the circle correspond to where the graph the 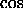 function has
maximum values and minimum values?
function has
maximum values and minimum values?
- What is the period of f? the amplitude of f?
- From the algebraic form of f, describe how to modify the graph
of
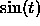 to obtain the graph of f. How do the modifications
reflect algebra? Plot the graph of f with the graph of
to obtain the graph of f. How do the modifications
reflect algebra? Plot the graph of f with the graph of 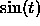 .
. - How many steps did you use in (b)? If you do them in a different order, do you get the same result? Explain.
- What is the period of g? the amplitude of g?
- From the algebraic form of g, describe how to modify the graph
of
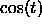 to obtain the graph of g. How do the modifications
reflect algebra? (Hint: Is this question really different from
2(b)?) Plot the graph of g with the graph of
to obtain the graph of g. How do the modifications
reflect algebra? (Hint: Is this question really different from
2(b)?) Plot the graph of g with the graph of 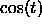 .
.
![]()
Using this identity and what we have done so far, describe the graph of
![]() in terms of the graph of
in terms of the graph of ![]() .
In particular, what are its period, amplitude and intercepts?
.
In particular, what are its period, amplitude and intercepts?