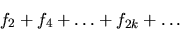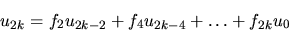Next: About this document ...
Up: No Title
Previous: Introduction
We had asked for the probability with which a random walk in the line
will pass through a given position. If this position is the origin,
we are asking for the probability of returning to the origin. Let us
make an attempt at answering this question.
Suppose x is a point in the integer lattice on the real line (fancy
language for x is an integer) and suppose n is the number of steps
in a random walk. We begin by considering n-step random walks.
- Compute the number Nn,x of n-step random walks that are at
location x after n steps. That is, calculate the number n-step
random walks with
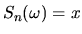 .
(It may help to write n = p +
q where p is the number of +1's appearing in the walk and q is
the number of -1's appearing in the walk up to this point.)
.
(It may help to write n = p +
q where p is the number of +1's appearing in the walk and q is
the number of -1's appearing in the walk up to this point.)
- Find the probability pn,x for an infinite random walk
 to
satisfy
to
satisfy
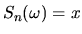 .
The case where x = 0 is of particular
use in this argument, so let us give it a separate label, un.
Notice, n must be even in this case. Why?
.
The case where x = 0 is of particular
use in this argument, so let us give it a separate label, un.
Notice, n must be even in this case. Why?
- As in the gambler's ruin problem, it will be useful to keep track
of the first return to the origin. Let f2k denote the probablity
of the first return occurring at step 2k, that is f2k is the
probability of
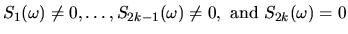 .
.
- Show that the probability that a random walk returns to the origin
is
- Show that the u's and the f's are related by
This will not be immediately useful to us, but we will be able to use it
further on in the discussion of random walks.
In order to proceed with the calculation of the probability of return to
the origin, we must express the f's in a simple fashion. This will be
accomplished in several steps. First, it will be useful to visualize a
random walk as a piecewise-linear graph of a function in the plane. The
graph is obtained by connecting the points
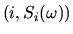 .
.



Next: About this document ...
Up: No Title
Previous: Introduction
2000-03-07