Exercises

1. This first game is a slightly simpler version of the coin flip game you played in Discussion 2. The first player, Rose, flips a coin. She can look at the coin, but she does not show it to Colin. She then can decide to play or fold. If she folds, she must pay Colin $2. If she decides to play, then Colin can decide to play or fold. If he folds, he pays Rose $2. If he decides to play both players look at the coin. If the coin is heads Rose wins $1 from Colin. If the coin is tails Colin wins $1 from Rose.
   1. If you were Rose, how would you play this game? What if you were Colin? Are there strategies you would not use?
   2. Since Colin does not know the result of the coin flip, he has only two possible strategies. On the other hand, since Rose can look at the coin in advance, she has four possible strategies. Describe Rose and Colin's strategies.
   3. The expected payoffs of this game depend on the coin flip. If we assume the coin is heads, what is the payoff matrix? (Remember this should be a 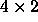matrix.) If we assume the coin is tails, what is the payoff matrix?
   4. How can we combine the two payoff matrices from part (b) into an expected payoff matrix for the game? (Hint: Rose would expect to get heads 50% of the time and tails 50% of the time, that is, the probability of flipping heads is 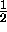and the probability of flipping tails is .)
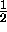   5. Solve this matrix game.
   6. Does your solution agree with how you would have chosen to play this game?
2. Suppose we change the stakes in the game from Exercise 1. In this game, let us assume that if Rose folds she still pays Colin $2 and if Colin folds he still pays Rose $2 but if they both decide to play they win $4 instead of $1.
   1. What is the expected payoff matrix for the new game?
   2. What are the optimal strategies for the players in this case?
   3. Explain how Rose's and Colin's strategies changed. Does this make sense in terms of the game?
3. Now let us consider the game from Discussion 2. Recall that in this game two players each put $5 on the table and each flip a coin. Neither player know the outcome of the other players coin flip. Player one, Rose, goes first. She can either pass or bet an additional $3. If she passes, the players compare their coins. If both are the same, each player takes their $5 back. If not, the player who flipped heads takes the $10. If Rose bets the additional $3, player two, Colin, can either see or fold. If Colin folds, Rose wins the $13. If Colin sees, he adds $3 to the money on the table and then the players compare coins. If they are the same, each player gets their money back. If not, the player who flipped heads takes the $16.

   In order to analyze this game as a two-person zero-sum game, we must determine the possible strategies for each player. Each player has four strategies. Rose can always bet, no matter what the coin flip is, always pass no matter what the coin flip is, bet if the coin is heads and pass if it is tails or pass if the coin is heads and bet if it is tails. Colin can always see, no matter what the coin flip is, can always fold, no matter what the coin flip is, can see if the coin is heads and fold if it is tails or can fold if the coin is heads and pass if the coin is tails.

   Thus Rose's strategies are :

   • A = always bet
   • B = always pass
   • C = bet for heads, pass for tails
   • D = pass for heads, bet for tails.

   Colin's strategies are:

   • A = always see
   • B = always fold
   • C = see for heads, fold for tails,
   • D = fold for heads, see for tails.
   1. If you were Rose, how would you play this game? If you were Colin, how would you play this game? Are there strategies that you would not use?
   2. The expected payoffs of this game depend on the coin flips. Write down the payoff matrix for each possible set of coin flips. (Thus you should have four 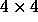matrices, one for two heads, one for two tails, one for heads and tails, and one for tails and heads.)
   3. Combine these payoff matrices to determine the expected payoff matrix for the game.
   4. Solve this matrix game to determine the value of the game and the optimal strategies.
   5. Suppose the stakes were changed so that if the players want to bet they must bet $10 instead of $3. Do the optimal strategies change? Explain.