CSCI 363 Computational Vision--Spring 2023

    Assignments

    Home | | Schedule | | Assignments | | Lecture Notes

    Assignment 6, Due Thursday, April 20

    This assignment contains two programming problems. In one you will create a movie to demonstrate the stereo-kinetic-effect, and experiment with parameters that affect the power of this effect. In the second, you will compute the optic flow field for a given set of observer motion parameters. The initial code for the programming problems are contained in the ~csci363/assignments/assign6 subdirectory on radius. After copying this folder to your own assign6 directory, set the Current Directory in MATLAB to this folder.

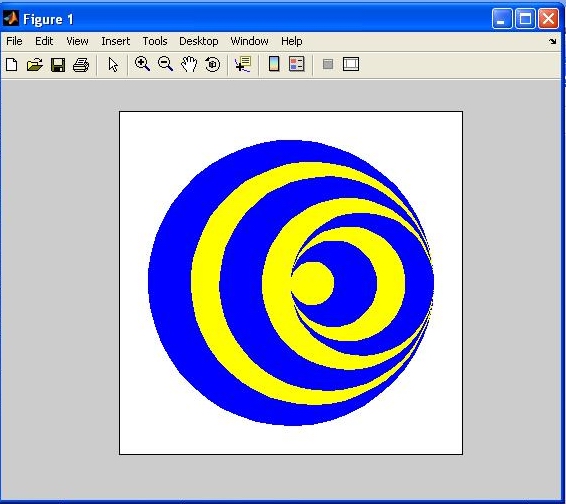
    Problem 1: The Stereokinetic Effect

    If an object simply undergoes pure rotation in the image plane, it does not generate 2-D image motion that can be used to recover its 3-D shape. There are some patterns, however, that yield a percept of 3-D shape when they are just rotating rigidly in the image. A particularly striking example of such a pattern is shown below. A movie of this pattern rotating can be found at a website developed by Michael Bach (http://www.michaelbach.de/ot/mot-ske/index.html). This phenomenon is known as the stereokinetic effect. In this problem, your first step will be to write a MATLAB function named ske that creates a movie of the pattern shown below, rotating around its center. This function can be implemented in a way that allows you to create a variation on this pattern that highlights the basis for perceiving 3-D shape from this moving image.

       

    Part a: Create a movie of the stereokinetic effect

    There are two functions related to this problem contained in the assign6 directory that you copied. The function circlePoints generates x,y coordinates of a set of points evenly spaced around a circle. The inputs to this function are the x,y coordinates of the center of the circle, the radius of the circle, and the number of sample points around its perimeter. This function returns two vectors containing the x and y coordinates. The ske function creates a movie of a yellow circle rotating inside a larger stationary circle as in the image below:

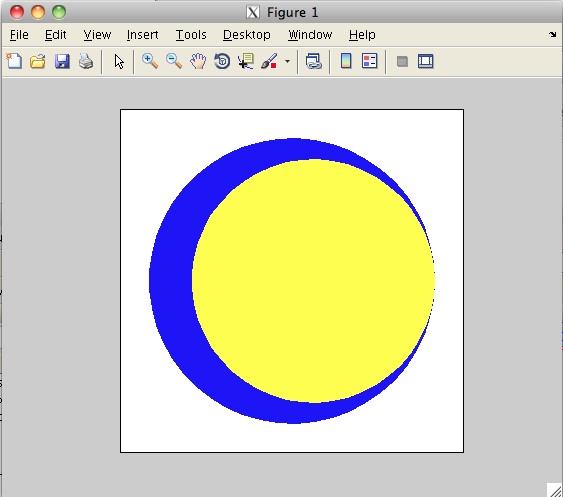
    The parameter npts specifies the number of points used to draw the circles. Smaller numbers of points (e.g. 10) will show polygons, rather than circles. Larger numbers of points (e.g. 50) will show smoother circles. The movie is a sequence of frames stored in a vector of MATLAB structures. This function uses two built-in functions, fill and getframe. The fill function draws a filled-in polygon, given the x and y coordinates of points around its perimeter. The getframe function creates a snapshot of the picture displayed in the current figure window. The built-in movie function can then be used to display the frames of the movie. The inputs to movie are a vector of structures containing the movie frames, the number of times to show the movie, and the rate of presentation of the frames, specified as the number of frames per second. The ske and movie functions can be called as shown below:

        >> skeMovie = ske(50);
        >> movie(skeMovie, 2, 10);

    Note: If you are logged in remotely, the movie will be very slow and not very smooth, particularly if you are not on campus. To see the full KDE, you should probably try logging in to one of the NUCs in the Swords 219 lab.

    Your assignment is to complete the ske(npts) function so that it shows the complete ske rotating figure as diagrammed in the first image above. Your ske function should return the frames of a movie in which the ske cone pattern is rotated around its center (for simplicity, the largest blue circle should be centered at the origin, (0,0)).

    Study the ske function to see how it works. Note that to create the movie, first a circle is created using circlePoints that describes the motion of the center of the inner yellow circle. In this case it is a circle of radius 15, centered at the origin. The coordinates of the center of this circle for each frame of the movie are stored in the vectors: xc1 and yc1, each of which contain 50 values. For each movie frame created inside the for loop, circlePoints is used to draw a circle of radius 85 around the center location, xc1(frame), yc1(frame), for that frame.

    To complete the image use the following parameters for the rotating circles:
    Circle numberRadius of motion of
    center coordinates    		Radius of circlecolor
    Circle 11585yellow
    Circle 22575blue
    Circle 34060yellow
    Circle 45050blue
    Circle 54040yellow
    Circle 63030blue
    Circle 72020yellow

    Note that the stationary outer blue circle is not included in the table. The first circle listed is the circle already in the ske function you downloaded. You must add the other 6 circles.

    Feel free to change the colors in the pattern - it is easiest to use the 8 basic colors that can be specified with a single character (r(red), g(green), b(blue), m(magenta), c(cyan), y(yellow), w(white) and k(black)).

    When you are done, turn in a hard-copy of your ske.m file, and upload a copy of the ske.m file to Canvas.

    Problem 2: Recovering Observer Motion

    Part a: The following equations specify the x and y components of the image velocity (Vx,Vy) as a function of the movement of the observer (translation (Tx,Ty,Tz) and rotation (Rx,Ry,Rz)) and depth Z(x,y):

        Vx = (-Tx + xTz)/Z + Rxxy - Ry(x2+1) + Rzy
        Vy = (-Ty + yTz)/Z + Rx(y2 + 1) - Ryxy - Rzx

    Write a function setupImageVelocities that computes the image velocity field that results from a movement of the observer:

    function [vx vy xfoe yfoe] = setupImageVelocities(Tx,Ty,Tz,Rx,Ry,Rz,zmap)

    The input zmap is a 2-D matrix of the depths of the surfaces that project to each image location. The output matrices vx and vy should be the same size as the input zmap. Assume that the origin of the x,y image coordinate system is represented at the center of the zmap, vx and vy matrices. The indices of these matrices should also be scaled to obtain the x and y coordinates that are used in the above equations. In particular, let i and j represent the indices of the zmap, vx and vy matrices (where i is the first (row) index and j is the second (column) index), and let icenter and jcenter denote the indices of the center location in these matrices (icenter is the middle row and jcenter is the middle column). Then the x and y coordinates that are used in the above expressions for Vx and Vy should be calculated as follows:

        x = 0.05*(i-icenter);
        y = 0.05*(j-jcenter);

    The setupImageVelocities function should also return the x and y coordinates of the focus of expansion, Tx/Tz and Ty/Tz (if Tz is 0, then this function can just return a value such as 1000.0 for the coordinates of the focus of expansion, to indicate that it is undefined in this case). The function displayVelocityField in the observer folder displays velocities at evenly spaced locations in the horizontal and vertical directions. It has three inputs that are the vx and vy matrices and the distance between the locations where a velocity vector is displayed. The foeScript.m code file contains some initial statements for testing your setupImageVelocities function and displaying the results. The depth map used in these examples consists of a central square surface at a distance of 25 from the observer, in front of a background surface at a distance of 100. There are three examples, and each velocity field is displayed in a separate figure window. The coordinates of the FOE's are also printed. You can expand on these examples to explore the appearance of the velocity field for different combinations of translation and rotation of the observer, and surface depths. Given the depths and image coordinates used in the initial examples, velocities with a reasonable range of speeds can be obtained if the translation parameters are specified in the range of about 0.0-0.5, and the rotation parameters are specified in the range of about 0.0-0.03.

    Turn in: Your file for setupImageVelocities.m

    Part b: In class, we discussed an algorithm for recovering the direction of motion of the observer that was proposed by Longuet-Higgins and Prazdny. This algorithm is based on the following observation. At the location of a sudden change in depth in the scene, the component of image motion due to the observer's translation changes abruptly in the image, but there is very little change in the component of image motion that is due to the observer's rotation. Furthermore, the vector difference between the two 2-D image velocities on either side of a depth change lies on a line that points toward the focus of expansion (the observer's heading point). The computeObserverMotion function in the observer folder implements a simple version of Longuet-Higgins and Prazdny's algorithm. At each image location, this function first determines whether there is a large change in 2-D velocity in the horizontal or vertical direction. If so, the vector difference in velocity in the horizontal or vertical direction contributes toward the computation of the observer's heading point. To determine this heading point, the function combines velocity differences from a large number of image locations. In particular, it finds the best intersection point of all of the lines containing large velocity differences. There are two tests of the computeObserverMotion function in the foeScript.m code file that are initially commented out. Each call to this function is followed with a statement (also initially in comments) that prints the values of the coordinates of the true heading point and the computed heading point for each example. The true and computed values can be compared to determine the accuracy of computed heading. Expand on the examples provided in the foeScript file to answer the following two questions:

    1. The calculation of the heading point degrades if the range of depths in the scene is reduced. Why is this the case?
    2. Does the calculation of the heading point change significantly if there is rotation of the observer during translation? Why do you think this is?

    Part c: Longuet-Higgins and Prazdny's algorithm assumes that the scene is stationary. In other words, the scene cannot contain objects that undergo their own motion in space. In general, if an object undergoes its own motion, the vector differences in velocity across the boundaries of the object may no longer point to the observer's true heading point. Consider the diagram below, which shows sample velocities in four regions around the border of a square surface that is placed in front of a background surface. Assume that the true heading point is located at the center of the square, as shown. All of the velocity vectors point away from the FOE, and the velocities inside the border of the square have larger magnitude because the central surface is closer to the observer. The vectors obtained by computing the difference between the velocities inside and outside the border of the square also have a direction that lies on a line through the FOE. Suppose that the central square undergoes its own motion, consisting of a constant translation of the square patch to the right, as shown by the arrow attached to the FOE. The final motion of each point on the central surface would then be the result of adding this constant rightward velocity to the velocity that results from the observer's translation.

    Turn in the following:

    1. Turn in a drawing for the following: For each of the four regions circled below, show how this added object motion would alter the difference in velocity measured across the border. Draw the lines that contain the four velocity difference vectors and show roughly where these lines intersect in the image (this is the heading point that would be computed by Longuet-Higgins and Prazdny's algorithm).
    2. Answer the following question: Can this algorithm compute the correct heading point for these situations where the object undergoes its own motion?

    Submission details:

    • Hand in a hardcopy of your ske.m file
    • Hand in a hardcopy of your setupImageVelocities.m file and
    • Hand in your written drawings and explanations for problems 2b and 2c.
    • Hand in your Discussion Log
    • Upload to Canvas the electronic copies of your ske.m and setupImageVelocities.m code files

    Home | | Schedule | | Assignments | | Lecture Notes

    Constance Royden--croyden@holycross.edu
    Computer Science 363--Computational Vision
    Last Modified: April 12, 2023
    Page Expires: April 12, 2024