Solution to Assignment 3

Problem 1: Flower Transform

There are many ways to solve this problem. Here is one solution:

C code for solution to flower transform problem

Problem 2: Reflection about a line

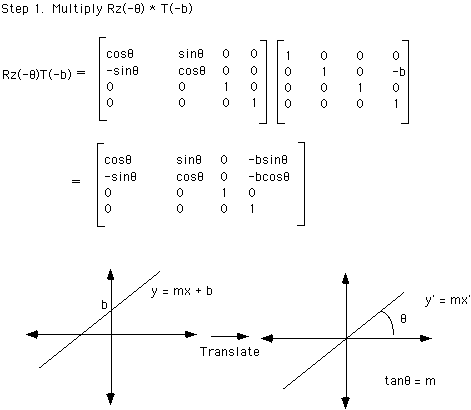
We perform the reflection about the line, y = mx + b in five steps:

1. Transform the line vertically to cross through the origin. This means translating it by -b units in the y direction. The matrix T(0, -b, 0) performs this translation.
2. Rotate the line so it coincides with the X axis. The angle, theta, between the line and the x axis is defined as: tan(theta) = y/x = m. Therefore, theta = arctan(m). The rotation is in the clockwise direction, so it is a negative rotation about the z axis. Use the matrix Rz(-theta) for this transformation.
3. Use the Scale matrix to reflect across the x axis.
4. Undo the rotation, using Rz(theta).
5. Undo the original translation, using T(0, b, 0).

M = T(0, b, 0)*Rz(theta)*S(1, -1, 1)*Rz(-theta)*T(0, -b, 0)

Where theta = arctan(m).

We can compute M by multiplying the matrices together, as follows.

Final Equations

x1 = x*cos(2*theta) + y*sin(2*theta) - b*sin(2*theta)

y1 = x*sin(2*theta) - y*cos(2*theta) + b*cos(2*theta) + b

z1 = z

Where theta = arctan(m)

Home | | Syllabus | | Assignments | | Documentation

Constance Royden--croyden@mathcs.holycross.edu
Computer Science 384
Date Created: August 17, 1999
Last Modified: October 5, 2003
Page Expires: August 17, 2004