Home | | Syllabus | |
Assignments | |
Documentation
Assignment 5
Due: Thursday, October 30, in class
Problem 1: Walking through a scene.
In this problem, you will implement a program to walk the camera through a scene,
very similar to the example given in section 5.7 of the textbook. Instead of walking
around a 3D cube, we will walk around the 3D pyramid that was developed in class.
Copy the
threeDpyramid.c code given here and paste it into
a source file. You will modify this program so that you will be able to move the
camera position with a keypress. Do this in three steps: First, convert the projection
to a perspective projection. Second, set the initial position of the camera. Third,
implement a keyboard function to change the viewing position using the gluLookAt() function.
Before you start, save the threeDpyramid.c file as username_lookAt.c.
Step 1. Change the projection from orthographic to Perspective.
Use the function, gluPerspective(fovy, aspect, near, far) to set up the perspective
projection clipping volume, where fovy is the vertical field of view (in degrees)
of the clipping
volume, aspect is the aspect ratio for the width/height, and near and far
indicate the
near and far clipping planes. Keep in mind that near = -zmin and far = -zmax. Thus, for
a clipping volume that can be seen by the camera (along the negative z axis), zmin and zmax
will be negative numbers but near and far are given as positive numbers. Set up the
perspective viewing so that fovy = 45 degrees, aspect = 1.0, near = 1.0 and far = 400.0. You
can call gluPerspective() from the myinit() function in place of the glOrtho() function
that we used for orthographic projections. You do not have to write a reshape function
as is shown in the book.
Don't look at the pyramid yet--It won't look good until you set up the camera position.
Step 2. Set the initial viewing position of the camera.
You will use the function gluLookAt(vx, vy, vz, atx, aty, atz, upx, upy, upz) to specify
the position and orientation of the camera. As we walk through the scene, we will always
point the camera at the origin (for this problem). So, (atx, aty, atz) = (0.0, 0.0, 0.0).
The up vector will be the Y axis: (upx, upy, upz) = (0.0, 1.0, 0.0). (vx, vy, vz) will
specify the camera position. Set up a global 3-element array, GLfloat viewer[3], to hold the
camera position (vx = viewer[0], vy = viewer[1], vz = viewer[2]. Initialize the array so
that vx = vy = 0.0 and vz = 250.0. In the display() function, add a line for
gluLookAt() to set the camera position (see example A.11 in the appendix of the book).
You should now be able to run your program and see the 3D pyramid rotating on the
screen.
Step 3. Add keyboard functions to walk through the scene.
Add a keyboard function to change the camera position along the x, y and z axes
when you press the x, y, and z keys (i.e. viewer[0], viewer[1] or viewer[2] will be
changed). Lower case x, y and z should decrement the
position by 1.0 along the appropriate axis (repeatedly as long as the key is held down)
and upper case should increment the position. You may use the keys() function from the
example in A.12 of the book. You should now be
able to view the pyramid and use the keys to reposition the camera. (You should
stop the spinning of the pyramid to get a better sense of the camera motion--you
can do this by setting the spin permanently to 0.0 in the code). Save the complete
code in the username_lookAt.c.
Part b. Questions about the perspective projection in the above problem.
1. If you used glFrustum(xmin, xmax, ymin, ymax, near, far) instead of gluPerspective()
in your program, what values of xmin, xmax, ymin and ymax would give you the same
clipping volume as specified in the program?
2. Why did you set the initial camera position with vz = 250.0? What would happen if
you had set it to vz = 0.0?
3. When you hit the lowercase 'z' key, the vz component is decremented, but the pyramid
appears to move toward the camera (i.e. it gets bigger), as if it is moving in a positive
Z direction. Why is this?
4. If you hold down the lower case 'x' key for a long time, the pyramid appears to move away
from the camera, i.e. it gets smaller. After a while, the top of the pyramid gets flattened
(Note: you will only see this if the pyramid is not spinning).
As the pyramid moves further away, the top gets flatter. Why does this happen?
Write the answers to the above questions and turn them in with the hardcopy of your
program.
Problem 2: A simple shadow projection.
In this problem we will use the projection technique discussed in lecture and in
section 5.10 of the book to create a shadow of the spinning pyramid on the x-y plane.
As with the above problem, we will start with the spinning pyramid.
Use the threeDpyramid.c source code to
start with. Paste it into a source code file and save it as username_shadow.c.
Use the following steps to create a shadow on the x-z plane.
Step 1. Set the position of the light source
Create a global variable that indicates the x, y and z position of the light source
(e.g. use a 3-element array). Set the position of the light source to (0.0, 250.0, 0.0).
The second element of this array should be used in the computation of -1/yl in matrix m
for step 2.
Step 2. Create the projections matrix, m.
Write an initialization function that sets up the projection matrix, m[16] that will
project the shadow along the y axis onto the x-z plane (as described in lecture
and in section 5.10 of the book). You can call this function from main(). Make
sure m is a global variable. Use the global variable from part 1 to calculate
-1/yl.
Step 3. Draw your pyramid
The pyramid should be rendered as in the original threeDpyramid.c display() function.
However, the following transformations should be applied:
- Scale the pyramid by 0.75 in x, y and z directions.
- Rotate the pyramid about the Y axis by the amount given by spin (as in the original code).
- Translate the pyramid upward by 100.0 units (in the positive Y direction).
- Rotate the pyramid by 30.0 degrees about the X axis.
Remember to list the transformations in the reverse order in which they will be applied
to the pyramid! The last transformation--the rotation about the x axis--is used so that
we will be able to see the x-z plane in the final rendering.
Step 4. Draw the shadow
Now you will redraw the pyramid as a projected shadow. First, use glPushMatrix() to
save the current transformation matrix. Then use glLoadIdentity() to get back to the
original state of the pyramid. You will want to apply the following transformations to
obtain the correct shadow of the pyramid:
- Do the first 3 transformations that were done for the pyramid object above.
- Translate the object so that the light source is at the origin: T(-xl, -yl, -zl).
- Multiply by the projection matrix, m.
- Translate back: T(xl, yl, zl).
- Rotate by 30.0 degrees about the X axis.
Again, remember to reverse the order of transformations in your code. Again, the last
rotation (about the X axis) is so that we can see the x-z plane. In orthographic projections,
a plane that is perpendicular to the projection plane is invisible. The final rotation rotates
the shadow and the pyramid so that the plane of the shadow is no longer perpendicular to the
viewing plane.
After the transformations are specified, re-draw all the faces of the pyramid. Make
sure to set the color to gray (red=green=blue= 0.3 works nicely). You should now have
a spinning pyramid with a shadow. Make sure to use glPopMatrix() at the end to return to the previous
model_view state. The following image shows one view of the spinning pyramid and its shadow:
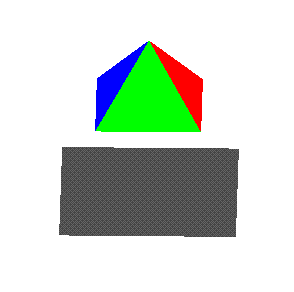
Save your code in the file username_shadow.c.
Turning in this assignment
Turn in a hardcopy of the C code for problems 1 and 2 and the answers to the questions
in problem 1. This
is due in class, Thursday, October 30.
In addition, email a copy of the files containing your C code to me at
croyden@mathcs.holycross.edu. The subject
line should read "Graphics Assignment 5". There should be 2 files named "username_lookAt.c", and
"username_shadow.c".
This should be emailed before class on the due date.
Home | | Syllabus | |
Assignments | |
Documentation
Constance Royden--croyden@mathcs.holycross.edu.edu
Computer Science 384
Date Created: August 17, 1999
Last Modified: October 21, 2003
Page Expires: August 17, 2004
|
