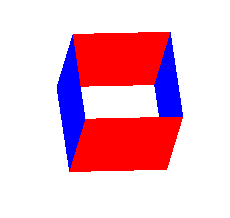Home | | Syllabus | |
Assignments | |
Documentation
Assignment 4
Due: Thursday, October 23, in class
Problem 1:
In this problem, you will use openGL functions to create a 3-Dimensional object
that rotates about different axes depending on a key-press. You will first create
a simple 3D box, open at the top and bottom, then you will add the code that allows it to rotate.
Finally, you will write a program that recursively divides each of the quadrilateral faces
into two new quads, generating the approximation of a cylinder (that is open at the top
and bottom).
Part a. A spinning box.
Write a program similar to the example program for a spinning 3D pyramid demonstrated
in lecture 12.
This program should create a box, with 4 quadrilateral faces (instead of the square-based
pyramid that was demonstrated in lecture) that is open at the top and bottom.
Make your box centered
on the origin. You should create the faces of the box so that the "outward" face is
toward the outside of the object. (Use the right-hand rule to make sure you list the vertices
in the correct order to accomplish this). Alternate the colors of the sides between red
and blue so
that you can see the
three-dimensionality of the box. Use an idle function to rotate the box
about the x or y axis so that you can see the different sides of it (just as we did in
lecture). Save this file as username_box.c. The following image shows the tetrahedron
viewed at an angle from the top:
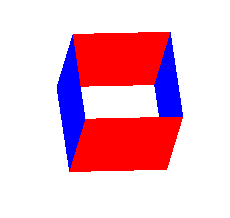
Part b. Add a user interface
Save the program you wrote in part a in a new file called, username_spin.c. Modify this
program to include a user-interface that detects a keypress. A press of the 'f' key should
cause the tetrahedron to spin about the x axis. The 'j' key should cause spin about the y
axis and the 'k' key should cause spin about the z axis. To respond to a keypress, use
the function: glutKeyboard(keys), where keys() is the callback function for a keypress. An
example of responding to a keypress is in the Moving Viewer program in appendix A.12 of the
textbook. That program also has a mouse function that controls spin about an axis with a
mouse-click. You will need to use the same logic in your keys() function that controls
the spin axis with a keypress. Save the code for this part in a file called username_spin.c
Part c. Approximating a cylinder
One way to generate a sphere in openGL, is by successively dividing triangular faces
of a polyhedron into more triangles, and normalizing all the vertices so that they lie
on the surface of a sphere. An example of this approach is described in the textbook
in section 6.6 and the program is given in appendix A.13>
In this part of the problem, you will use a recursive strategy similar to that
in example A.13 of the textbook (the Sphere program) to approximate a cylinder. Instead
of using the divide_triangle function to recursively divide the object into triangular
faces, you will write a recursive divide_quad() function that will recursively divide
the quadrilateral faces of your box into 2 new quadrilateral faces.
Save the code from part b in a new file, called
username_cylinder.c. First, you will need to normalize the vertices of your
box so that they all lie an equal distance from the y axis. If a vertex is at
position (x, y, z), and you want it to be a distance, d, from the y axis, you can normalize
by multiplying each component by d/(sqrt(x*x + z*z)). Make sure none of your vertices
is at the point (0, 0, 0) before doing this!. Second, create a recursive
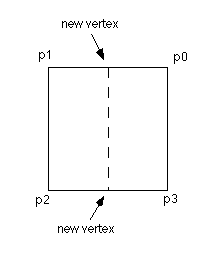
function, divide_quad(), that takes four vertices and an integer counter as parameters.
divide_quad() should calculate two new vertices from the four given as parameters, one at
the center of the top edge and one at the center of the bottom edge. These new vertices
should then be normalized
to be at the same distance from the y axis as the others. The new vertices, along with pairs
of the other four vertices, define 2 new quadrilaterals as shown below.
If the recursive counting variable is greater than zero, these two new quads should
be divided (by calling divide_quad with the new sets of vertices). This is then repeated
for as many levels as defined by the counter. (I recommend trying small numbers, like 0, 1 and 2
levels, to test it out). When the counter reaches zero, render the current quadrilateral
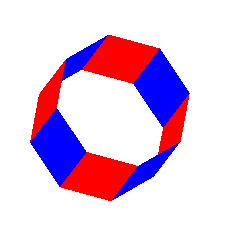
from the four vertex parameters. Below is the resulting object for m=1, viewed at an angle
from the top.
You will need to specify a unique color for each face of your cylinder. I recommend
alternating the color between two primary colors such as red and blue. You can do this
by setting the color to red before one call to divide_quad() and to blue before the
second call to divide_quad(), and so on.
Part d. Optional Extra Credit (worth up to 20 pts)
Modify your program from part c to either create a more interesting object than a tetrahedron
box, cylinder or sphere (worth 1 pt) or to make the tetrahedron (or object) do a more interesting animation
than simply rotating around an axis when you hit the 'd' key (worth 1 pt). For example, it could do a little
dance or it could turn on its head and hop around. I will base the score on good programming
technique and originality. Have some fun with this part. Save your program in a file called
username_extraCredit.c.
Problem 2: Gimbal Lock
If you followed the example given in A.12 of the book to make your box rotate about the three
different coordinate axes, you will notice that the rotations are performed about each of the
axes in turn:
glRotatef(theta[0], 1.0, 0.0, 0.0); //Rotate about X axis
glRotatef(theta[1], 0.0, 1.0, 0.0); //Rotate about Y axis
glRotatef(theta[2], 0.0, 0.0, 1.0); //Rotate about Z axis
This implementation leads to an interesting phenomenon, known as gimbal lock, which
occurs in the following situation. If the user presses a key (the 'j' key) to rotate
the object by 90 deg
about the Y axis, then subsequent rotations about the X or Z axis will appear to have the
same effect--i.e. the object will appear to rotate about the same axis for either key press.
(The rotation is actually in opposite directions, but it is hard to see that with the 3D box
or cylinder). What is going on here?
Your task is to show that gimbal lock is a direct consequence of the calls to glRotatef()
in the display function. Note that the program will perform the rotations in the same order
(First about Z, then about Y and finally about X) when drawing the object, independent of
the order in which the user pressed the keys. Use the matrix equations for the transformations
involved in the three glRotatef() calls to show that the sequence Rz(theta)Ry(90)Rx(0) is equivalent
to the sequence Rz(0)Ry(90)Rx(-theta). (You need to do the matrix multiplication on this one to
show that the results are the same). Write out the matrix equations and their solutions.
Problem 3: Camera Position based on Yaw, Pitch and Roll.
In section 5.3.4 of the textbook, the concept of Yaw, Pitch and Roll are defined in terms
of an aircraft. If the airplane is pointing along the Z axis, then yaw is a rotation
about the y axis, pitch is rotation about the x axis and roll is rotation about the z axis. Note that
the "camera" in this case is in the nose of the plane, which is not centered at the origin.
Given three angles, theta1, theta2, and theta3 that define the amount of yaw, pitch and roll,
respectively, and a distance d of the nose of the airplane from its center of mass (located
at the origin), write the matrix multiplication equation that sets up the camera in the viewing
position that corresponds to the yaw, pitch and roll (in that order). Hand in the equation,
showing the complete matrices that are multiplied together. You do not need to multiply out
these matrices.
Turning in this assignment
Turn in a hardcopy of the C code for problem 1, and your solutions for problems 2 and 3. This
is due in class, Thursday, October 23.
In addition, email a copy of the files containing your C code to me at
croyden@mathcs.holycross.edu. The subject
line should read "Graphics Assignment 4". There should be 3 files
named "username_box.c",
"username_spin.c", "username_cylinder.c" and (if you have it) "username_extraCredit.c".
This should be dropped before the due date.
Home | | Syllabus | |
Assignments | |
Documentation
Constance Royden--croyden@mathcs.holycross.edu.edu
Computer Science 384
Date Created: August 17, 1999
Last Modified: October 14, 2003
Page Expires: August 17, 2004
|