

Next:About
this document ...
Odyssey Mathematics Workshop
Friday, August 23
Mathematics in the Computer Lab
-
We will be using a program called Maple, developed at the University
of Waterloo in Canada. This program can be used in the Haberlin 408 PC
lab. If you want to use the printer in this lab, you will first have to
log into the college network; otherwise, you can just close any login windows.
-
To start Maple, double click on the maple leaf icon ``Maple V Release 5''.
-
Commands in Maple are entered after the > sign, and must end with
a semicolon ;
-
To define a function f(x), start with
f := x ->
(make the arrow with a dash - and > sign). After
the arrow, enter the rule for the function. For example, to define the
function f(x) =
x2
- 3x + 5, enter
f := x -> x^2 - 3*x + 5;
note that we use ^ for exponents and * for multiplication.
-
Once a function is defined, we can evaluate it, solve equations involving
it, and plot it. For example, to compute f(3) for the function f(x)
which you defined, type
f(3);
Check the answer by hand.
-
You are not restricted to ``f'' and ``x'' - function and
variable names can be almost anything you want, and you can substitute
any expression into a function. Try
f(holycross);
-
To solve an equation such as x2
- 3x + 5 = 17, type
solve(f(x)=17,x);
How did Maple solve the equation? How many solutions are there?
If you want the solutions in decimal form, put a decimal point after the
17:
solve(f(x)=17.,x);
-
To plot the graph of f, type
plot(f(x),x=-3..3);
This plots the graph in the range 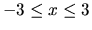 .
Notice that the scales on the x and y axes are different,
and that the scale on the y-axis does not start at zero. How can
you visualize one of the solutions to f(x) = 17 on the graph?
.
Notice that the scales on the x and y axes are different,
and that the scale on the y-axis does not start at zero. How can
you visualize one of the solutions to f(x) = 17 on the graph?
-
There are various plotting options which can be changed. Click on the plot
with the left mouse button to select the plot window, then try some of
the options in the ``Style'' menu or the toolbar at the top of the screen.
-
The vertex of the parabola we plotted is at x = 1.5. To get a more
symmetric picture, we can change the x-range so that it is centered
at 1.5, say
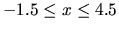 ,
and restrict the y-range to
,
and restrict the y-range to 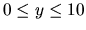 by
entering
by
entering
plot(f(x),x=-1.5..4.5,0..10);
-
Define another function g(x)
= x2 - 3x + 1. To plot f and g on
the same axes, use
-
plot({f(x),g(x)},x=-1.5..4.5,0..10);
You are now ready to work on the lab.
Assignment 3 (Lab)
First draft due at the end of class Friday
Answer briefly, but use complete sentences. Illustrate with rough sketches
where appropriate. Do not hand in any printed Maple output.
1. What is the relationship between the functions f and
g
which you defined above? What is the relationship between their graphs?
2. Using Maple, define and plot the three functions 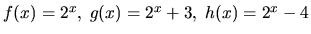 .
Plot these simultaneously in the range
.
Plot these simultaneously in the range 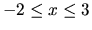 ,
, 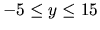 .
What relationship do the graphs have to each other?
.
What relationship do the graphs have to each other?
3. If f,g are two functions such that g(x)
= f(x) + c where c is a constant (possibly
negative), how is the graph of g related to the graph of f?
4. Using Maple, define the function f(x)
= x3 - 3x + 1. Then define the function g(x)
= f(x + 1). That is, replace x in the rule for f
by x + 1. The simplest way to do this on Maple is (once you have
defined f)
g := x -> f(x + 1);
Write out g as a sum of powers of x.
5. Plot f,g from problem 4 on the same axes, in
the range 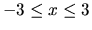 .
What is the relationship between their graphs?
.
What is the relationship between their graphs?
6. Using Maple, define the function 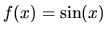 .
Then define the function g(x)
= f(x - 2). Plot both in the range
.
Then define the function g(x)
= f(x - 2). Plot both in the range 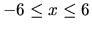 and determine the relationship between their graphs.
and determine the relationship between their graphs.
7. If f,g are two functions such that g(x)
= f(x + c) where c is a constant (possibly
negative), how is the graph of g related to the graph of f?
8. Investigate the effect of the transformation which replaces
x
by -x. That is, let g(x)
= f(-x) and compare the graphs of f and g,
as you did in the previous problems. You may use different functions than
the ones used above. You do not have to write down all your intermediate
steps. The goal is to use your observations to complete the following sentence:
``The effect on the graph of f(x) of replacing f(x)
by f(-x) is ... ''. You should illustrate your answer with
at least one example.
9. As in problem 9, but investigate the effect of the transformation
which replaces f(x) by -f(x). That is, let g(x)
= -f(x), etc.
10. An even function is one for which f(x)
= f(-x). An odd function is one for which f(x)
= -f(-x). Classify the following functions as even, odd,
or neither. One way to do this is to plot the functions and use your answers
from problems 9 and 10. Another way is simply replace x by -x
in the formula for f and see how the formula changes.
-
a.
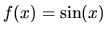
-
b.
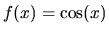
-
c. f(x) = x3
- x
-
d. f(x) = x3
- x + 1
-
e. f(x) = x4
- 3x2 + 2
-
f. f(x) =
x4
- 3x3 + x + 2
-
g. f(x) = 2x.


Next:About
this document ...
John Anderson
2001-08-01
![]() .
Notice that the scales on the x and y axes are different,
and that the scale on the y-axis does not start at zero. How can
you visualize one of the solutions to f(x) = 17 on the graph?
.
Notice that the scales on the x and y axes are different,
and that the scale on the y-axis does not start at zero. How can
you visualize one of the solutions to f(x) = 17 on the graph?