MATH 371 -- Numerical Analysis

October 15 -- Polynomial Interpolation, Cubic Spline Interpolation

For "nice" functions like cos( x ) on small intervals, we can see that

the error of interpolation -> 0 as n -> . For instance, using the

bound 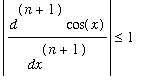, the following is an upper bound on the

interpolation error using the n th degree polynomial:

> CosErrorBound:=(n,x)->1/(n+1)!*product(abs(x-j/n),j=0..n);

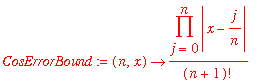
The larger n is, the smaller this error bound is:

> plot(CosErrorBound(5,x),x=0..1);

> plot(CosErrorBound(10,x),x=0..1);

> plot(CosErrorBound(20,x),x=0..1);

Note the scales on the y- axes(!) If we plot the interpolating polynomial together with

cos( x ) on [0,1], the difference is already invisible with n = 5:

> with(CurveFitting):

> IP:=x->PolynomialInterpolation([seq(evalf(j/5),j=0..5)],[seq(evalf(cos(j/5)),j=0..5)],x);

> plot({IP(x),cos(x)},x=0..1);

If the interval is not small, and/or the function is not "nice", then the

picture can be entirely different.

Next, let's try an interpolating polynomial for , which is "nice" by almost

any criterion. BUT, let's use x = 1,2,3,4,5, so the interval is not so small .

> IP2:=x->PolynomialInterpolation([1.,2.,3.,4.,5.],[exp(1.),exp(2.),exp(3.),exp(4.),exp(5.)],x);

To see how closely our interpolating polynomial matches the exponential function at other points we can either compute a few values:

> IP2(1.35); exp(1.35);

> IP2(1.62); exp(1.62);

Note the agreement is not so close any more!

The actual error versus the theoretical error bound for polynomial interpolation in this case,

using the upper bound M = for the 5th derivative of on [1,5]:

> plot({abs(exp(x)-IP2(x)),abs((exp(5)/24)*(x-1)*(x-2)*(x-3)*(x-4)*(x-5))},x=1..5,y=0..23);

In this case again, taking more interpolation points will help, though

> ExpErrorBound:=(n,x)->abs(exp(5)/n!*product(x-(1+4*(j/n)),j=0..n));

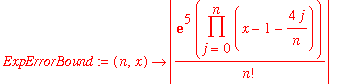
> plot(ExpErrorBound(10,x),x=1..5);

And taking n -> will make the error bound go to zero on the whole

interval.

Other shapes of graphs are just very difficult for polynomials to approximate

well . An example is graphs with horizontal asymptotes, if we take a large

interval. For instance, if we wanted to interpolate a function like:

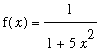
> f:=x->1/(1+5*x^2);

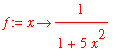
> xlist:=n->[seq(evalf(-3+6*j/n),j=0..n)];

> ylist:=n->map(f,xlist(n));

> xlist(10);

> ylist(10);

> IP3:=n->PolynomialInterpolation(xlist(n),ylist(n),x);

Here are the interpolating polynomials of degrees 4,8,12,16 plotted together with y = f( x ):

> plot({f(x),IP3(4)},x=-3..3);

> plot({f(x),IP3(8)},x=-3..3);

> plot({f(x),IP3(12)},x=-3..3);

> plot({f(x),IP3(16)},x=-3..3);

>

In fact, we can see that the error near the ends of the interval is growing with n,

not decreasing. The technical name for this phenomenon is `` polynomial wiggle ''.

One "way around" these problems is to use a different approach to interpolation.

Instead of trying to use a single polynomial of high degree to approximate a function

like this over a large interval, it certainly seems to be better to use a piecewise-polynomial

function -- one defined by different polynomial formulas on different segments of its

domain. One of the most popular choices here is to use ``cubic splines'' -- piecewise

cubic polynomial functions. We will see in class next time that there is enough freedom

in cubic polynomials to be able to construct a function defined by cubics

on [ ] for i = 0,1,2, ... , n-1, satisfying:

1) , = f( ) for i = 1, ..., n -1, and

so is a continuous function interpolating the points ( ), i = 0, 1, ... , n,

2) S' ( x ) is continuous -- the derivative of at is the same as the derivative

of at for i = 0,1,..., n -2

3) S'' ( x ) is continuous -- the second derivative of at is the same as the

second derivative of at for i = 0,1,..., n -2, and

4) Either: S'' ( ) = 0 and S'' ( ) = 0 (``free or natural spline''), or

S' ( ) = a and S' ( ) = b for arbitrary a, b (``clamped spline'')

The CurveFitting package also contains a routine that computes free cubic splines. Here

is a first example, using the same function and the same interpolation points as in the

last examples. The output shows the piecewise cubics:

> IS:=x->Spline(xlist(10),ylist(10),x);

> plot({IS(x),f(x)},x=-3..3);

Note that the results do not show the same kind of ``wiggle problems'' that the

high degree interpolating polynomials showed(!)