MATH 392 -- Geometry Through History
Euclid's Proof of the Pythagorean Theorem (Proposition I.47 of the Elements)
The following animations give the idea behind Euclid's ingenious
and elegant proof of the Pythagorean Theorem from Proposition 47 in
Book I of the Elements. Note: Many historians of mathematics
believe that this proof was probably an original contribution of Euclid
since this proof does not appear elsewhere in ancient Greek mathematical
texts.
The red figures are the squares on the sides of a given right triangle
(a 3-4-5 right triangle with hypotenuse along the x-axis).
The dashed blue line shows a perpendicular dropped from the vertex
opposite the hypotenuse to the hypotenuse. Extended, this line
subdivides the square on the hypotenuse into two rectangles. The
idea of the proof is to show that the square on the other sides of
the right triangle have areas equal to these two rectangles. Establishing
this will show that the square on the hypotenuse is equal to the
sum of the squares on the other two sides, which is Euclid's form
of the theorem.
| > |
Maple Commands
| > |
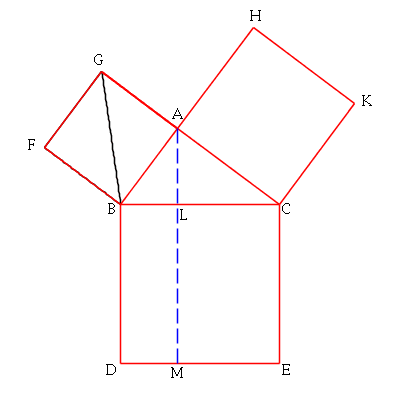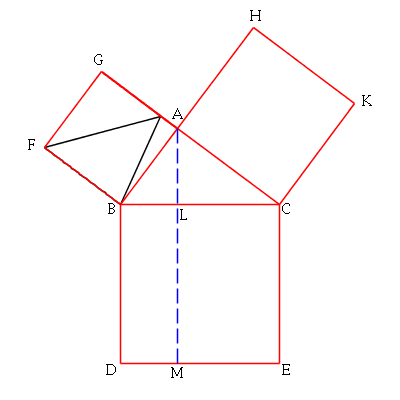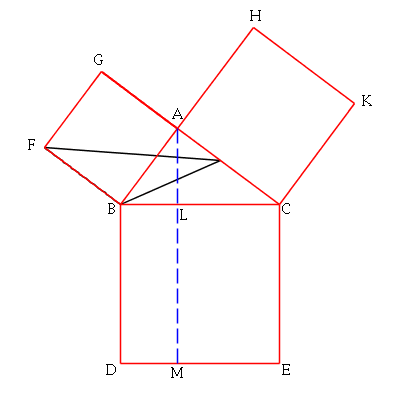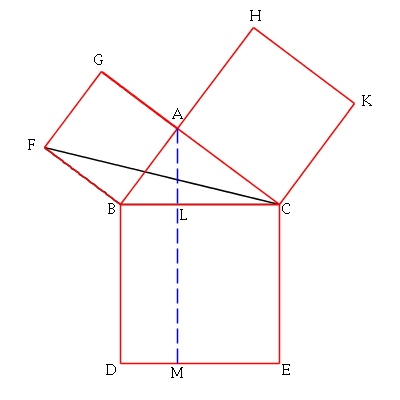 |
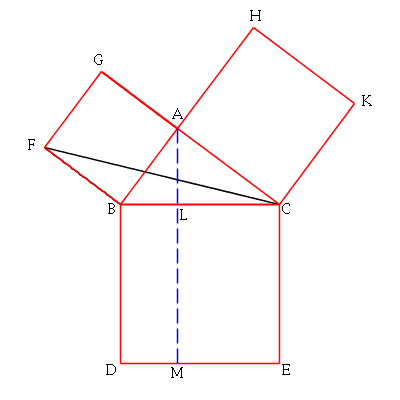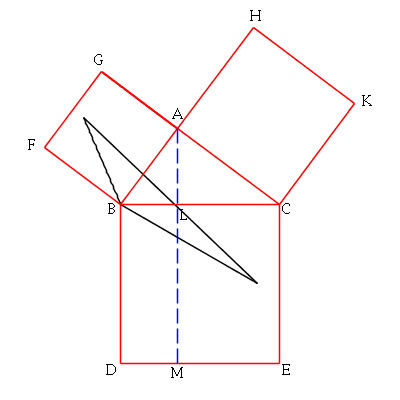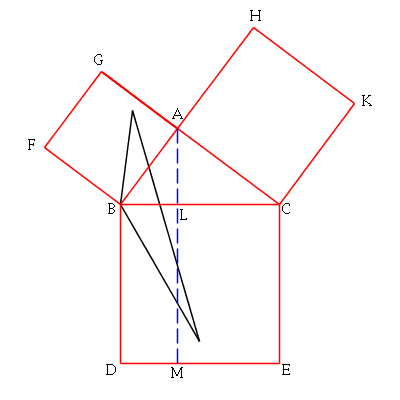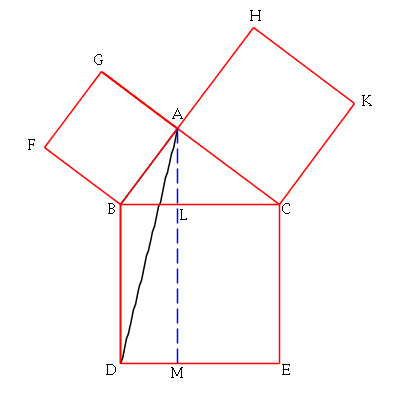
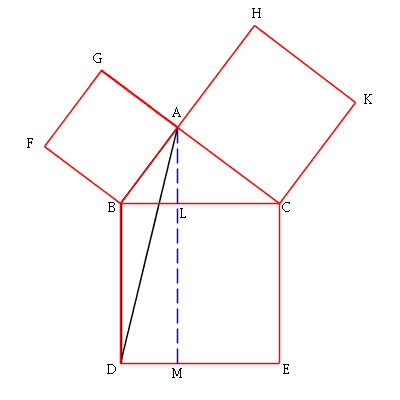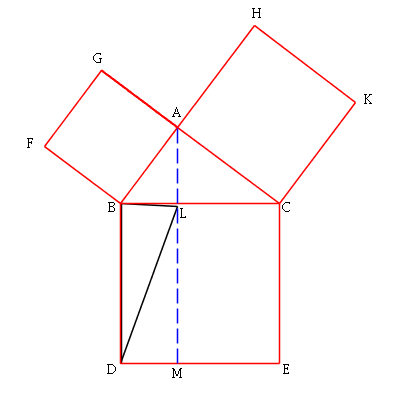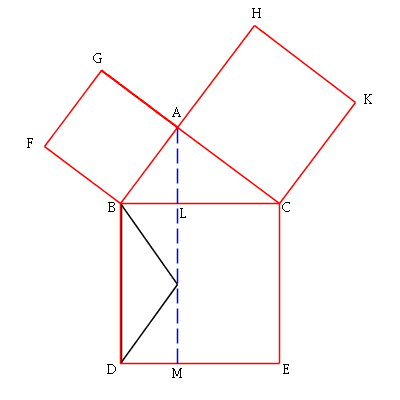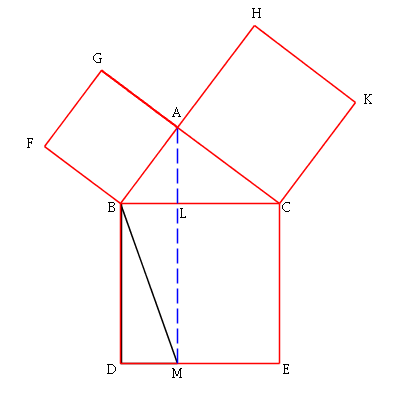
In the first animation (above), consider the black triangle that is
formed by a diagonal of the square to the left of the blue line.
We keep the base along a side of the small square, but slide
the upper vertex along the parallel line. From Proposition I.37, we
know that all these triangles have equal area. We continue sliding
the upper vertex until it reaches the far end of the hypotenuse.
(The animation is "looped," though so the whole process repeats.)
The next animation rotates the final position of the black triangle by
90 degrees clockwise about the point B, demonstrating visually that
triangles FBC and ABD are congruent:
| > |
 |
Using Proposition I.37 again, we slide one vertex along the dashed blue
line until it reaches the bottom of the rectangle on the left. All of these
triangles also have the same area.
| > |
 |
| > |
The final triangle is half of the left rectangle. Hence half of the
small square equals half that rectangle. So the whole square also
equals the whole rectangle.
Finally, we do a similar argument with the other square and the rectangle
on the right of the blue line (not shown, but the idea is the same!) to finish
the proof. Pretty nifty!