Modeling1.html

MATH 136 -- Advanced Placement Calculus

Logistic Models with Harvesting (Environmental Modeling)

November 24, 2009

The logistic equation and the solution with Q(0) = 1.3 Mg

(1)

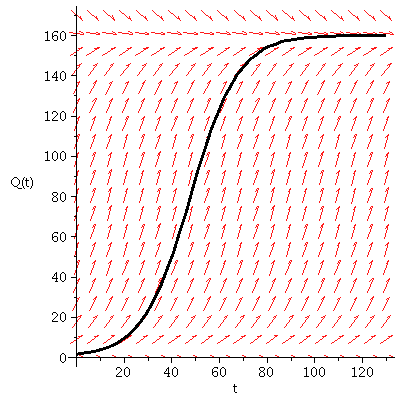Plot_2d

The formula for the solution of the logistic equation is:

(2)

(3)

(4)

These are the biomass values at the times t = 0, 10, 20, ... , 150 years:

(5)

The recovery time is the time it takes the forest to regrow to 99% of the carrying capacity, or (.99)(160) = 158.4:

(6)

Thus the recovery time is about 94 years.

The "virgin state" would be represented by the initial value Q(0) = 160.

Harvesting Strategy 1: With 3.2 Mg of biomass harvested each year, the differential equation becomes:

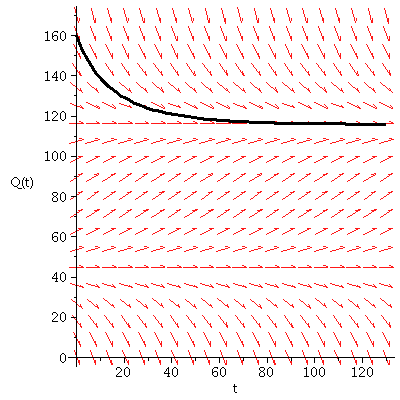Plot_2d

Note that the solution seems to be tending to a limiting value of about Q = 116 as
Harvesting Strategy 2: With the harvesting level at 6.4 Mg/year, the differential equation becomes

(7)

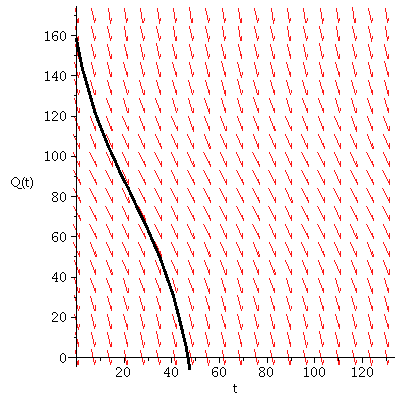Plot_2d

The solution reaches the value Q = 0 at about t = 47 years. At that time, all the biomass in the forest has been removed (the forest has "crashed").

To find the equilibria of these differential equations with the harvesting terms, we need to

set the right-hand sides equal to zero and solve for Q. This can be done in Maple as follows.

For the harvesting level of 3.2 Mg/year, we use:

(8)

in the plot of the solutions for the equation with the harvesting level of 3.2 Mg/year above. The solutions tend toward the 115.78 level, they

tend away from the 44.22 level. These values can also be derived by using the quadratic

formula to solve this quaratic equation

for Q:

> (-.1 + sqrt((.1)^2 - 4*(-1/1600)*(-3.2)))/(2*(-1/1600));

(9)

(10)

On the other hand, with the harvesting term 6.4 Mg/year, the quadratic equation

(11)

has no real roots, so there are no equilibria.

The maximum sustainable harvesting level is exactly 4.0 Mg/year (per hectare). This

can be seen algebraically, since the largest value of h for which the quadratic equation

has real roots is when so h = 4.