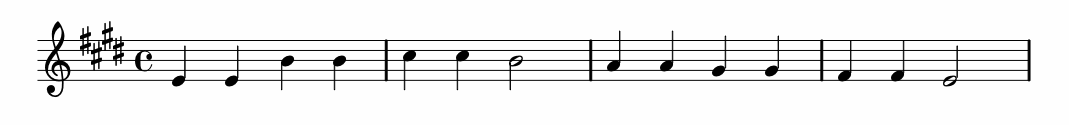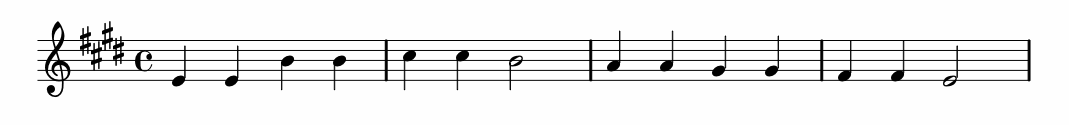Below are some types of questions you can expect to find on the exam. This is certainly not an exhaustive list and is meant to give a general overview. For a more detailed list of topics, see the Midterm Exam Review sheet.

Questions:

1. Listening Questions: Upon listening, be able to identify, using both musical and mathematical terminology, what type(s) of symmetry is present in a piece (CD #1). You should also be able to identify the composer of the piece being played.


2. Take the first 4 bars of Twinkle Twinkle Little Star in the key of E major and write the inversion about G#, staying in the key of E major (use the treble clef). Also write the retrograde-inversion, inverting about G#, staying in the key of E major (use the treble clef).



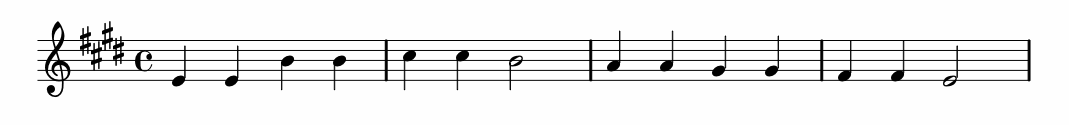
3. Take the first 4 bars of Twinkle Twinkle Little Star in the key of E major and write the exact inversion about G# in the treble clef, using correct accidentals.


4. Give three musical examples (title and composer) where the mathematical symmetry of a horizontal reflection is used. What is the musical name of this symmetry?


5. Give three musical examples (title and composer) where the mathematical symmetry of a vertical reflection is used. What is the musical name of this symmetry?


6. Explain why the integers do not form a group under multiplication.


7. Suppose a piece of music is both a retrograde and an exact inversion about the middle of the staff. What other type of symmetry must it necessarily possess? Explain using concepts from group theory. What if the exact inversion is about a note not located on the middle of the staff?


8. Give an example of a group that is non-commutative, that is, there are elements a and b where a*b ≠ b*a.


9. Consider the set S of odd integers ±1, ±3, ±5, . . . Is the set S closed under addition? Is S closed under multiplication? Does S form a group if * = multiplication? Explain.


10. Consider the group G = {0, 1, 2, 3} with * = addition modulo 4 (e.g., 2 * 3 = 1 since 2 + 3 = 5 and 5 - 4 = 1.) Construct the multiplication table for G and state the inverse of each element. What group (or subgroup) does this remind you of?


11. What are the first 12 Fibonacci numbers? What is the recursive relationship that defines the sequence of Fibonacci numbers? What is the golden ratio and how is it related to the Fibonacci numbers? Where do the Fibonacci numbers arise in nature?


12. If φ is the golden ratio, find and simplify the quantities φ², φ³ - 1, and φ⁴ - 3φ. Do these without a calculator!


13. What are the three mandatory rules in change ringing necessary for a legitimate extent? What does it mean from a mathematical viewpoint for an extent to satisfy the "palindrome property"?


14. Write out a full extent on n = 3 bells. How many different extents on 3 bells are there? Explain.


15. Write out the first 8 changes of Plain Bob Minimus. What is the connection between these changes and the symmetries of the square?


16. How many different ways are there to arrange 12 bells if the odd numbered bells are fixed? In other words, Bell 1 stays as Bell 1, Bell 3 stays as Bell 3, etc. A sample arrangement is (1 12 3 10 5 8 7 6 9 4 11 2).


17. How many permissible moves (permutations) are there on 10 bells? Recall that a permissible move is one that only interchanges adjacent bells.


18. Given the permutations a = (2 3 5 4 1) and b = (4 2 3 1 5), compute a*b, b*a, b³ and a^-1.


19. Suppose that a and b are elements of a group (neither of which is the identity element) and that a⁴ = e, b² = e and b a b = a. What is the inverse of a? What is the inverse of b? Show that a b = b a. Simplify the quantities a²⁰¹⁵ and (a b)⁵.