9: Activities - How to get started Exploring

• Example Activity (Adjacent Angles)
• Angles
• General Triangles
• Isosceles Triangles
• Equilateral Triangle
• Right Triangles
• Congruent Triangles
• Rectangles & Squares
• Parallelograms
• Rhombus
• Polygons
• Circles
• Tessellations of the Plane

Many of the items in the "Help" menu present a set of statements that are theorems in Euclidean Geometry. Your job is to determine which of the statements are also theorems in Hyperbolic Geometry.

For example, the following statement is a theorem in Euclidean Geometry:

Euclidean Theorem:

The adjacent angles formed by a pair of intersecting lines are supplementary, and together measure 180°.

To do this, first construct three or four random pairs of intersecting lines. Next, plot a point at the intersection of each pair of lines. There are two different ways you can plot the intersection points. The inaccurate way is to select the "Plot Point" command, move the mouse to the point where the lines cross, and click. This method is inaccurate because it is unlikely that you will succeed in getting the mouse exactly on the intersection point. The accurate method is to select the "Plot Intersection Point" command from the "Constructions" menu. Either way, once you have plotted the intersection point, then use the "Measure Angle" command from the "Measurements" menu to measure the two angles in each pair of adjacent angles.

If you succeed in constructing a counter example, then you have proved the Euclidean Theorem about adjacent angles false in Hyperbolic Geometry. Failing to construct a counter example does not prove anything; however, if, after many tries, you fail to construct a counter example, then the statement is likely to be true in Hyperbolic Geometry. .

Note: be aware of rounding.  When the "Measure Angle" command reports that an angle is 45.5° it might actually be 45.4817331°.

MEASURING AN ANGLE IN NONEUCLID:
You can measure a Hyperbolic angle by selecting the "Measure Angle" option from the "
Measurement" Menu.

ACTIVITY:   The following is a list of theorems about intersecting lines in Euclidean Geometry.  Which (if any) are true in Hyperbolic Geometry?

1. The adjacent angles formed by a pair of intersecting lines are supplementary and together measure 180° (this was done in the example exercise).
2. Vertical angles are congruent.

ACTIVITY:     The following is a list of theorems about Triangles in Euclidean Geometry.  Which (if any) are theorems in Hyperbolic Geometry?

1. The sum of the angles of a Triangle is 180 degrees.
2. The longest side of a Triangle is opposite the greatest angle.
3. All three altitudes of a Triangle intersect in a single point.   (Hint:  To construct an altitude of a triangle, use the "Draw Perpendicular" command from the "Constructions" menu.  Click the mouse on any two vertices to define the base.  Then click on the third vertex to draw the altitude.)
4. In a triangle, the sum of any two sides is always greater than the length of the third side.
5. In a Triangle, if one of the sides is extended, the exterior angle is greater than either of the opposite interior angles.
6. In a Triangle, the product "base times height" is the same regardless of which side is chosen as the base. For example, in triangle ABC, (AB) x (the height to C) = (BC) x (the height to A).

ACTIVITY:     The following is a list of theorems about Isosceles Triangles in Euclidean Geometry.  Which (if any) are theorems in Hyperbolic Geometry?

It is possible to construct an Isosceles Triangle. (Hint: to prove this statement is true, you must construct a figure that fits the definition -- a triangle that has two sides of the same length.)

1. The base angles of an Isosceles Triangle are congruent.
2. The altitude of an Isosceles Triangle bisects the vertex angle and the base.

ACTIVITY:     The following is a list of theorems about Equilateral Triangles in Euclidean Geometry.  Which (if any) are theorems in Hyperbolic Geometry?

1. It is possible to construct an Equilateral Triangle.
2. An Equilateral Triangle is also Equiangular (all three angles have equal measure).
3. Each angle of an Equilateral Triangle measures 60 degrees.

ACTIVITY:     The following is a list of theorems about Right Triangles in Euclidean Geometry.  Which (if any) are theorems in Hyperbolic Geometry?

1. It is possible to construct a Right Triangle.
2. The Pythagorean Theorem -- In any Right Triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the legs.

ACTIVITY:

1. A good way to explore properties of Congruent Triangles is to:
• Construct a triangle.
• Construct an infinite line.
• Use the Reflect command from the Constructions menu to reflect each of the sides of your triangle across the infinite line.   This reflected triangle will be congruent to your original triangle; however, since it is in a different part of the Hyperbolic plane , it will appear to have different curvature.
• Use the Move command from the Edit menu to move the vertex points of the original triangle you constructed in step (a) or move the Infinite line you constructed in step (b).  The reflection of the triangle will also move.
• Try making a reflection of a reflection of a reflection of a reflection.  Move the original vertexes and watch a cool animation of congruent triangles.
2. SSS, and SSA are both theorems in Euclidean Geometry, are they theorems in Hyperbolic Geometry?
3. In Euclidean Geometry, either ASS nor AAA, is sufficient to prove a pair of triangles congruent.  Is either ASS or AAA sufficient to prove triangles congruent in Hyperbolic Geometry?

DEFINITION:     A Rectangle is a quadrilateral with four 90° angles.

DEFINITION:     A Square is a Rectangle with four sides of equal length.

DEFINITION:     A Regular Quadrilateral is a quadrilateral in which all of the angles have equal measure and all of the sides have equal length.

ACTIVITY:

1. In Hyperbolic Geometry, rectangles do not exist, and, therefore, neither do squares.  In Hyperbolic Geometry, if a quadrilateral has 3 right angles, then the forth angle must be acute.  Construct an example of this.

1. It is possible to construct a Regular Quadrilateral.
2. All regular quadrilaterals have four right angles.
3. The two lines passing through the midpoints of the opposite sides of a regular quadrilateral divide the regular quadrilateral into four smaller regular quadrilaterals.
4. The diagonals of a regular quadrilateral bisect each other.
5. The diagonals of a regular quadrilateral are perpendicular.

ACTIVITY:      The following is a list of theorems about Parallelograms in Euclidean Geometry.  Which (if any) are theorems in Hyperbolic Geometry?

1. It is possible to construct a Parallelogram.
2. The opposite sides of a Parallelogram have equal length.
3. The opposite angles of a Parallelogram have equal measure.
4. The diagonals of a Parallelogram bisect each other.

ACTIVITY:      The following is a list of theorems about Rhombi in Euclidean Geometry.  Which (if any) are theorems in Hyperbolic Geometry?

1. It is possible to construct a Rhombus.
2. The opposite angles of a Rhombus are congruent.
3. The diagonals of a Rhombus bisect each other.
4. The diagonals of a Rhombus are perpendicular.
5. The diagonals of a Rhombus bisect the Rhombus's angles.

DEFINITION:     A Regular Polygon is a Polygon in which all of the angles have equal measure, and all of the sides have equal length.

ACTIVITY:

1. Which of the following Regular Polygons can you construct with NonEuclid?
• regular triangle
• regular quadrilateral (4 sides)
• regular pentagon (5 sides)
• regular hexagon (6 sides)
• regular heptagon (7 sides)
• regular octagon (8 sides)
• regular nonagon (9 sides)
• regular decagon (10 sides)
• regular dodecagon (12 sides)
2. In Euclidean Geometry, any Polygon can be completely enclosed in some sufficiently large triangle. This is so obvious a statement that I have never even seen it written as a theorem.  In, Hyperbolic Geometry, this is not an obvious statement.   Is it a true statement?
3. In Euclidean Geometry, any Regular Polygon can be inscribed in a circle.  Is that true in Hyperbolic Geometry?
4. In Euclidean Geometry, any Regular Polygon can be circumscribed in a circle.  Is that true in Hyperbolic Geometry?

Notice that "having a round shape" is not part of the definition of a Circle.  Personally, I find it very interesting that circles happen to appear round in both Euclidean and Hyperbolic geometry.

ACTIVITY:

1. In Hyperbolic Geometry, construct a Circle and 8 radii of the Circle.
2. In Euclidean Geometry, through any three, non collinear points there passes a circle.  Is this a theorem in Hyperbolic Geometry? Why or why not?

   Recall that the standard construction in Euclidean geometry for circumscribing a triangle is:

   1. Let A, B, and C be three non-collinear points.
   2. Construct line segments joining the three non-collinear points (forming a triangle).
   3. Construct the perpendicular bisector of any two of the sides of the new triangle (pick sides AB and BC).
   4. Let X be the intersection of the two perpendicular bisectors.
   5. Construct the circle with center at X that passes through A.
   6. Construct segments AX, BX, and CX (we want to show that these are radii of the constructed).
   7. The length of segment AX must be the same as the length of segment BX because they are corresponding sides of congruent triangles (use SAS – midpoint, right angle, and reflexive).
   8. Likewise, BX must be the same length as CX.
   9. Since AX = BX and BX = CX, all three lengths are equal.
   10. Therefore, since a circle is the locus of points equal distant from a given point, and since A, B, and C are all the same distance from point X, a circle centered at X that passes through one of these must pass through all three.

   If the above construction does not work in Hyperbolic geometry, then it must be because at least one of the steps depends on the Parallel Axiom.

   Can you find the rub? In which step does it lie?

   Hint: Perform the above circumscription in NonEuclid. Then use the MOVE POINT command from the EDIT menu to move one of the vertices of the original triangle. Your answer will jump into existence (literally). Note: It looks cooler if you construct all three perpendicular bisectors rather than just the two descried in the construction.

3. In a Euclidean Geometry Circle, the ratio of Circumference/Diameter = pi. In Hyperbolic Geometry, is this ratio a constant for all circles, and if so is that constant equal to 3.141592654....   Hint: Just as in Euclidean Geometry, in Hyperbolic Geometry, the circumference of a circle can be given upper and lower bounds by the perimeters of circumscribed and inscribed regular polygons. As the number of sides of the regular polygon increases, the polygon's perimeter becomes an increasingly closer approximation to the circle's circumference. Use NonEuclid to construct and measure the perimeter of a series of circumscribed and inscribed polygons.

In Euclidean Geometry, a square can be used to tessellate the plane; circles, however, will not tessellate the plane.

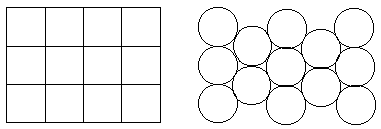
Figure 9-13-1

The Dutch artist, M.C. Escher [1902-1972], created many beautiful tessellations. Figure 9-13-2 is a low resolution copy of Escher's woodcut titled "Geckos" which is a tessellation of the Euclidean Plane.  Escher also worked extensively with non-Euclidean geometeries. In particular, his "Circle Limit" series are all tessellations of the Hyperbolic plane. Figure 9-13-3, titled "Heaven and Hell" is one of the works of the "Circle Limit" series. The demons and angles are each inscribed in congruent Hyperbolic triangles. The full size print is really quite attractive.

  
Figure 9-13-2: Tessellation of the Euclidean plane and of the Hyperbolic plane by M.C. Escher

Use NonEuclid to create your own tessellate the Hyperbolic plane using congruent Hyperbolic triangles. Print the tessellation and color it - inscribing some figure or pattern of figures in each triangle. The triangles used by Escher in "Heaven and Hell" are equilateral (thus it is a regular tessellation). Can the hyperbolic plane be tiled with other types triangles? Can it be tiled with any set of congruent triangles?

NonEuclid Home
Next Topic - Basic Concepts: What is Non-Euclidean Geometry