
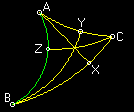
Figure 6.1: Altitudes of a Triangle
Triangle ABC is a Scalene triangle. Segments AX, BY, and CZ are the three altitudes of triangle ABC. Notice that, as in Euclidean Geometry, the three altitudes intersect at a single point. Measuring this particular triangle gives the following data:
6.2 A=s²
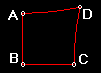
In Euclidean Geometry, we define a square region that has edges of
length 1 unit to have an area of 1 square unit. In Hyperbolic
Geometry, rectangles (quadrilaterals with 4 right angles) do not exist,
and, therefore, squares (a special case of a rectangle with four congruent
edges) also do not exist. In Hyperbolic Geometry, if a quadrilateral
has 3 right angles, then the forth angle must be acute (see figure 6.2a).
A regular quadrilateral is a quadrilateral that has four sides of equal length, and four angles of equal measure. A square it is a special case of regular quadrilateral where the four angles are right angles. In Euclidean Geometry, all regular quadrilaterals are squares. In Hyperbolic Geometry, regular quadrilaterals exist, but they all have four acute angles. Regular quadrilaterals in Hyperbolic Geometry cannot be used to form the basic unit of area the way squares do in Euclidean Geometry. One reason for this is that Hyperbolic, regular quadrilaterals do not fit together without leaving gaps. Figure 6.2b shows how nine, 1x1, Euclidean, regular quadrilaterals form a single 3x3, Euclidean, regular quadrilateral. Figure 6.2c shows five, 1x1, Hyperbolic, regular quadrilaterals - notice the gap in the upper right.

6.3 Defect of a Triangle
As we saw earlier, in Hyperbolic Geometry, the sum of the three angles
of a triangle is always less than 180°. The defect of a
triangle is defined as 180° minus the sum of the three angles of the
triangle. When we construct a few Hyperbolic triangles, and measure
the defect of each, we find that for small triangles the defect is small
(the angle sum is almost 180°). In fact, as the perimeter of
triangle approaches zero, the angle sum approaches 180°. This
is consistent with the idea that a relatively small piece of Hyperbolic
Space looks, and behaves very much like Euclidean Space. Contrariwise,
we find that large triangles have a large defect. As
the length of the three sides of a triangle get closer and closer to infinity,
each of the angles gets closer and closer to zero degrees - and, therefore,
the defect gets closer and closer to 180°.
Before proceeding, it would be a good idea to try constructing some example triangles in NonEuclid. Use the "Measure Triangle" command from the "Measurement" menu: this command will display the angle measure of each vertex, and the length of each side. It is important to get a "feel" for how it is that large triangles have large defects.
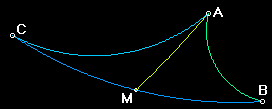
The larger the triangle, the larger the defect - but more than that: just like area, the defect is additive. The whole equals the sum of the parts. For example, in figure 6.3, the defect of triangle BAM is 77.4°, the defect of triangle CAM is 43.7°, and the defect of triangle ABC is 121.1° (77.4 + 43.7 = 121.1). This works for all triangles in Hyperbolic Geometry - regardless of how you cut them into smaller triangles. Use NonEuclid to try a few examples.
6.4 Defect of a Polygon
Any polygon can be cut up into a finite number of non-overlapping triangles.
Figure 6.4 shows two different ways that the same polygon might be cut
up.
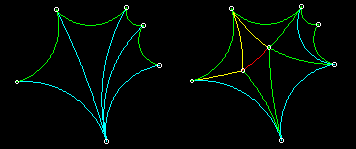
Figure 6.4: Two Different Decompositions
of a Polygon
The defect of a polygon is defined to be the sum of the defects
of a set of triangles that it can be cut up into. A polygon can be
cut up into triangular regions in infinitely many ways (to save space,
only two are shown for the polygon above). However, the sum depends
only on the polygon that we started with, and is independent of the way
in which we cut it up. Try constructing and measuring a few examples.
6.5 Invariance of Defect with
Translation
We have already seen, that objects appear to shrink, and flatten as
they move from the center of the Boundary Circle toward the edge.
Whatever we use to measure area must remain invariant as an object moves
from one location to another. Recall that in spite of the fact that
objects appear to shrink and flatten, the length of all sides, and the
measure of all the angles remains constant as an object moves. Therefore,
the defect remains constant as an object moves (since the defect is calculated
by measuring angles only).
6.6 Properties Necessary for
an Area Function
n summery, an area function must have the following properties [Moise-74]:
The choice of the constant, k, is important. It is what links
the units of length to the units of area.
6.7 Upper Bound to Area
One interesting consequence of A=kd, is that the maximum area of any
triangle is bounded. Since the defect of a triangle can never be
greater than 180°, the area can never be greater than k(180).
Is it also true that the area of a polygon is bounded? It could be
argued that the area of a polygon would have to be bounded as follows:
lets say that you constructed a polygon a defect of 200°. Then
construct a triangle that completely includes the polygon. The defect
of the triangle equals the sum of the defects of each of its parts, therefore
the defect of the triangle must be greater than 200° - but this is
impossible. Therefore, it must be impossible for a polygon to have
a defect of 200°. This however, is not a proof because it contains
an assumption - see the exercises on Polygons for more details.